Question

A brass rod of length 1m area $1m{m^2}$ and Young's modulus $120 \times {10^9}N/{m^2}$ is connected with steel rod of length $1{\text{m}}$ area $1m{m^2}$ and Young's modulus $60 \times {10^9}N/{m^2}$. Then the net stress so that extension of system is $0.2mm$
(a) $2 \times {10^6}N/{m^2}$
(b) $4 \times {10^6}{\text{N/}}{{\text{m}}^2}$
(c) $8 \times {10^6}N/{m^2}$
(d) $16 \times {10^6}N/{m^2}$

Answer 1

The stress-strain curve is linear at near-zero stress and strain, and Hooke's law that says stress is proportional to strain explains the relationship between stress and strain. Young's modulus is the proportionality coefficient. To produce the same amount of tension, the higher the module, the more stress is needed; an idealized rigid body will have an infinite Young's module. Conversely, without force, a very soft substance, such as a jelly, will deform.Since two rods in a series are connected. As they are joined end to end, the number of individual ones would be the complete extension. Also, for combined material, the area will be the same as each of these, say $A$; and force will also be the same.First, of all we will calculate the equivalent constant of the combined material ${k_{eq}}$ . Then we use the formula $F = {k_{eq}}\left( x \right)$ to calculate net stress and net stress is given by, $\dfrac{F}{A}$.

Complete step by step answer:

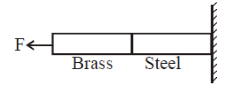
Given: For Brass rod– ${l_1} = 1m,{A_1} = 1m{m^2},{Y_1} = 120 \times {10^9}N/{m^2}$ , $x = 0.2nm = 0.2 \times {10^{ - 3}}m$
For steel rod– ${l_2} = 1m,{A_2} = 1m{m^2},{Y_2} = 60 \times {10^9}N/{m^2}$
For Brass rod, ${k_1} = \dfrac{{{Y_1}{A_1}}}{{{l_1}}} = \dfrac{{120 \times {{10}^9} \times A}}{1} = 120 \times {10^9} \times A$
For steel rod, ${k_2} = \dfrac{{{Y_2}{A_2}}}{{{l_2}}} = \dfrac{{60 \times {{10}^9} \times A}}{1} = 60 \times {10^9} \times A$
$\Rightarrow{k_{eq}} = \dfrac{{{k_1} \times {k_2}}}{{{k_1} + {k_2}}} = \dfrac{{120 \times {{10}^9} \times 60 \times {{10}^9} \times {A^2}}}{{120 \times {{10}^9}A + 60 \times {{10}^9}A}}$
$\Rightarrow{k_{eq}} = \dfrac{{120 \times {{10}^9} \times 60 \times {{10}^9} \times A}}{{120 \times {{10}^9} + 60 \times {{10}^9}}}$
$\Rightarrow{k_{eq}} = \dfrac{{120 \times 60 \times A}}{{120 + 60}} = \dfrac{{7200 \times {{10}^{18}} \times A}}{{180 \times {{10}^9}}}$
${k_{eq}} = 40 \times {10^9} \times A$
$\Rightarrow F = {k_{eq}}\left( x \right)$
$\Rightarrow F = 40 \times {10^9} \times A \times 0.2 \times {10^{ - 3}}$
$\therefore\dfrac{F}{A} = 8 \times {10^6}N/{m^2}$
Therefore, $\dfrac{F}{A} = 8 \times {10^6}N/{m^2}$.Hence,option (C) is the correct option.

Additional information:
Young's modulus is a mechanical property that tests a rigid material's stiffness. In the linear elasticity region of any axial deformation, the relationship between stress (force per unit area) and strain (proportional deformation) in a material is established.When a minimal load is applied to it in compression or expansion, a rigid object may undergo elastic deformation. Elastic deformation is reversible (after the load is lifted, the material returns to its original shape).

Note: In above question, formula ${k_{eq}} = \dfrac{{{k_1} \times {k_2}}}{{{k_1} + {k_2}}}$ for series connection is used. Different formula is used for parallel connection of two rods. So, it is confusing only about formulas used for series and parallel connection.