Question

A boy whose eye level is 1.3 m from the ground, sports a balloon moving with the wind in a horizontal level at some height from the ground. The angle of elevation of the balloon from the eyes of the boy at any instant is ${60^ \circ }$. After 2 seconds, the angle of elevation reduces to ${30^ \circ }$. If the speed of the wind at that moment is $29\sqrt 3 m/s$, then find the height of the balloon from ground.

Answer 1

Draw a corresponding diagram. Find the distance travelled by the balloon in 2 seconds where speed of the wind is $29\sqrt 3 m/s$. Then, use trigonometric properties in two right triangles formed to find the height of the balloon from the eye level. Then, add it with the given height of the boy to find the height of the balloon from ground.

Complete step-by-step answer:
Let $P$ be the position of the boy.

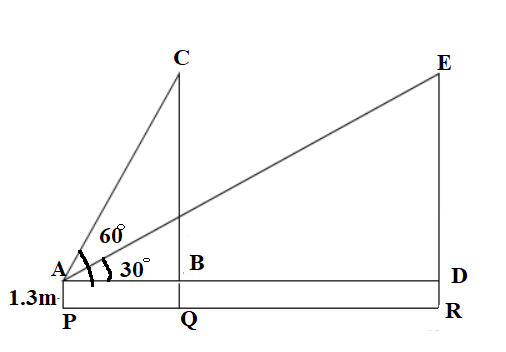
Then, the distance of $AP$ is 1.3m
Let the balloon moved from $C$ to $E$, which will also be equal to B to D
We are given that the speed of the wind is $29\sqrt 3 m/s$.
It is known that $\operatorname{distance} = {{speed \times time}}$
Hence, the distance travelled by the balloon in 2 seconds will be $29\sqrt 3 \left( 2 \right) = 58\sqrt 3 m$
Consider $\Delta ABC$
Here,
$\tan 60 = \dfrac{{BC}}{{AB}}$
And we know that $\tan 60 = \sqrt 3$
Then,
$\sqrt 3 = \dfrac{{BC}}{{AB}}$
$\Rightarrow AB = \dfrac{{BC}}{{\sqrt 3 }}$ eqn. (1)
And also, $\tan 30 = \dfrac{{DE}}{{AD}}$
We know that $\tan 30 = \dfrac{1}{{\sqrt 3 }}$
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{DE}}{{AD}}$
From the figure, we can see $AD$ is the sum of $AB$ and the distance travelled by balloon in seconds , that is $58\sqrt 3 m$.
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{DE}}{{AB + 58\sqrt 3 }} \\\ \Rightarrow \sqrt 3 \left( {DE} \right) = AB + 58\sqrt 3 \\\$
$\Rightarrow AB = \sqrt 3 \left( {DE} \right) - 58\sqrt 3$ eqn. (2)
From equation (1) and (2), we will get,
$\dfrac{{BC}}{{\sqrt 3 }} = \sqrt 3 \left( {DE} \right) - 58\sqrt 3$
From the figure, $BC = DE$
$\dfrac{{BC}}{{\sqrt 3 }} = \sqrt 3 \left( {BC} \right) - 58\sqrt 3 \\\ \Rightarrow BC = 3BC - 174 \\\ \Rightarrow 2BC = 174 \\\$
Divide both sides by 2.
$BC = 87m$
We will add the height of the boy to the $BC$ to find the height of the balloon from the ground $87 + 1.3 = 88.3m$.
Note: Many students make mistakes by not adding the height of the boy to the height of the balloon from the level of the height. But, we have to find the height of the balloon from the ground. Students must know the trigonometric ratios and the value of angles of trigonometric ratio, like $\tan 60,\tan 30$,etc.