Question
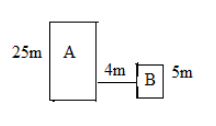
Question: A boy wants to jump from building \(A\) to building \(B\). Height of the building \(A\) is \(25m\) a...
A boy wants to jump from building A to building B. Height of the building A is 25m and that of building B is 5m.Distance between buildings is 4m.Assume that the body jumps horizontally, then calculate minimum velocity with which he has to jump to land safely on building B.
A. 6m/s
B. 8m/s
C. 4m/s
D. 2m/s
Solution
In this question, first we will discuss about the second law of equation of motion and then find the time taken to jump and then use the horizontal distance to calculate the minimum velocity required to jump safely from building A to building B.
Complete step by step answer:
It is given that the boy wants to jump from building A to building B.The height of the building A is 25m and the height of the building B is 5m. The distance between the two buildings is 4m.The boy jumps horizontally.Let say the boy jumps at a velocity Vm/s.Hence the vertical velocity of the boy is 0 and the horizontal velocity is Vm/s as the boy jumps horizontally.
Now the vertical distance between the two buildings is 25−5=20m.
So we know the second law of equation of motion S=ut+21at2 [where S is the distance, u is the initial velocity, t is time and a is acceleration due to gravity]
So the initial velocity of the boy is 0, a=10m/s2, S=20m the distance boy has to jump.
20=0×t+21×10t2
After simplification we will get,
t=2s
The boy needs 2secto jump from building A to building B.Now the horizontal distance is 4mand the horizontal velocity is Vm/s.
So, we can say that
Vt=4 ⇒V=t4 ⇒V=24 ∴V=2m/s
So the minimum velocity to jump safely from A to building B is required 2m/s.
Hence option (D) is correct.
Note: As we know that acceleration is a vector quantity that has magnitude and direction. As the boy is falling down so the acceleration due to gravity is in the same direction of gravity so here acceleration is taken as positive.
