Question

A boy stands at $78.4m$ from a building and throws a ball which just enters a window $39.2m$ above the ground. Calculate the velocity of projection of the ball.

Answer 1

In the question they have given maximum height and range of projection for the body which is there in projectile motion. By using the given data we will find the angle of projection then substituting in the equation of range of projection we will find the initial velocity of the body.

Formulas used:
Maximum height, ${H_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ ……………..$\left( 1 \right)$
Range of projection, $R = \dfrac{{{u^2}\sin 2\theta }}{g}$ ……………..$\left( 2 \right)$

Complete step-by-step solution:

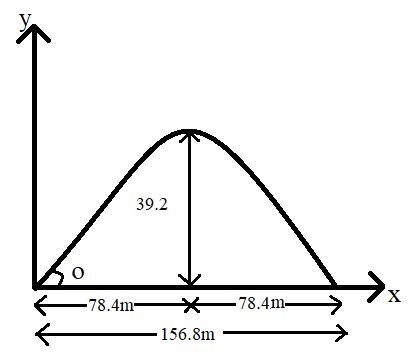
Given:
Range of projection, $R = 78.4m + 78.4m = 156.8m$
Maximum height , ${H_{\max }} = 39.2m$
Take, acceleration due to gravity , $g = 9.8m{s^{ - 2}}$
Using equation $\left( 1 \right)$
That is, ${H_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
$39.2 = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2 \times g}}$ …………… $\left( 3 \right)$
Using equation $\left( 2 \right)$
That is, $R = \dfrac{{{u^2}\sin 2\theta }}{g}$
$156.8 = \dfrac{{{u^2}\sin 2\theta }}{g}$ …………………$\left( 4 \right)$
$156.8 = \dfrac{{{u^2}2\sin \theta \cos \theta }}{g}$ ……………. $\left( 5 \right)$ $\left[ {\because \sin 2\theta = 2\sin \theta \cos \theta } \right]$
Divide equation $\left( 3 \right)$ and equation $\left( 5 \right)$
$\dfrac{{39.2}}{{156.8}} = \dfrac{{\dfrac{{{u^2}{{\sin }^2}\theta }}{{2 \times g}}}}{{\dfrac{{{u^2}2\sin \theta \cos \theta }}{g}}}$
$4 = \dfrac{{\dfrac{{\sin \theta }}{2}}}{{\dfrac{{2\cos \theta }}{1}}}$
Therefore, $\tan \theta = \dfrac{4}{4}$
$\tan \theta = 1$
$\theta = {\tan ^{ - 1}}1$
$\theta = {45^ \circ }$
Substituting in equation $\left( 4 \right)$ we get
$156.8 = \dfrac{{{u^2}\sin 90}}{{9.8}}$
$u = \sqrt {1536.64}$
Therefore, $u = 39.2m{s^{ - 1}}$

Note: Projectile motion is the form of motion experienced by a launched body that is motion of a body which is projected or thrown into the air with the angle made by the object with respect to the ground or x-axis.