Question

A boy pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2 N on the ring and rolls it without slipping with an acceleration of $0.3m/{s^2}$. The coefficient of friction between the stick and the ring is $\left( {\dfrac{P}{{10}}} \right)$ . The value of P is

Answer 1

There is pure rolling, we can solve this question by writing the torque equation about the instantaneous axis of rotation. We will also be using the parallel axis theorem to calculate the moment of inertia about the point of contact between the ground and the ring.

Complete step by step answer:
Here, we are having pure rolling, that means the point in contact with the ground will have zero velocity at the given moment but the point in contact with the stick will be slipping, so kinetic friction will be acting on the point. Thus, we can say that on the ground we have static friction and on the stick we have kinetic friction.
Now, let ${a_c} = 0.3m/{s^2}$i.e., acceleration of the center of the ring and the force applied by the stick on the ring will be 2 N as shown in the figure.
Since the ring is rotating towards the right, we can say that it is rotating in an anti-clockwise direction. So, the point of contact between the ring and the stick will be moving upwards, as a result, friction on the stick $\left( {{f_s}} \right)$ will be acting downwards.

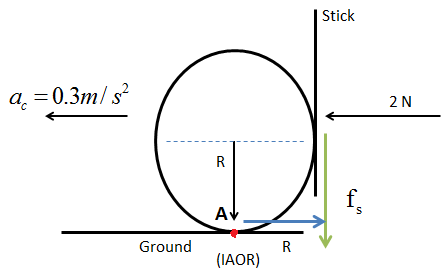
Now, the instantaneous velocity of the point on the ground will be zero. From the figure, we can say that the point A is the instantaneous axis of rotation. The instantaneous axis of rotation passes through a point perpendicular to the ring.
Now, the angular acceleration of the ring $\left( \alpha \right)$ (in case of pure rolling) will be:
$\alpha = \dfrac{{{a_c}}}{R}$
$\Rightarrow \alpha = \dfrac{{0.3}}{{0.5}}$
$\Rightarrow \alpha = 0.6rad/{s^2}$
Now, in case of pure rolling we can write the torque equation about the instantaneous axis of rotation, point A.
The stick will apply torque in the anti-clockwise direction and the ground will apply torque in the clockwise direction.
${\tau _A} = 2R - {f_s}R$
$\left( {{f_s} = \dfrac{P}{{10}} \times 2 = \dfrac{P}{5}} \right)$
$\Rightarrow {\tau _A} = 2R - \dfrac{P}{5} \times R$
$\Rightarrow {\tau _A} = 2(0.5) - \dfrac{P}{5} \times (0.5)$
$\Rightarrow {\tau _A} = 1 - \dfrac{P}{{10}}$
Now, we will find the moment of inertia about point A using the parallel axis theorem.
${I_A} = {I_C} + m{R^2}$
$\Rightarrow {I_A} = m{R^2} + m{R^2}$
$\Rightarrow {I_A} = 2m{R^2}$
$\Rightarrow {I_A} = 2 \times 2 \times 0.5 \times 0.5$
$\Rightarrow {I_A} = 1kg{m^2}$
Now, ${\tau _A} = {I_A}\alpha$
On substituting the values, we get
$1 - \dfrac{P}{{10}} = 1 \times 0.6$
$\Rightarrow P = 4$

Note: When you are reading the question it is always advisable to draw the diagram in parallel, in this way you can quickly collect the data and save yourselves some time. Writing torque equations about the instantaneous axis of rotation is not valid for all sorts of combined problems but only in the case of pure rolling, we can write the torque equation about the instantaneous axis of rotation. It is not applicable for general motions.