Question
Question: A boy of mass m with his mass centred at height H is standing in a train moving with constant accele...
A boy of mass m with his mass centred at height H is standing in a train moving with constant acceleration a. If his legs are wide spread with a distance 2d and he is not taking the help of any support then normal reactions at his feet are given by
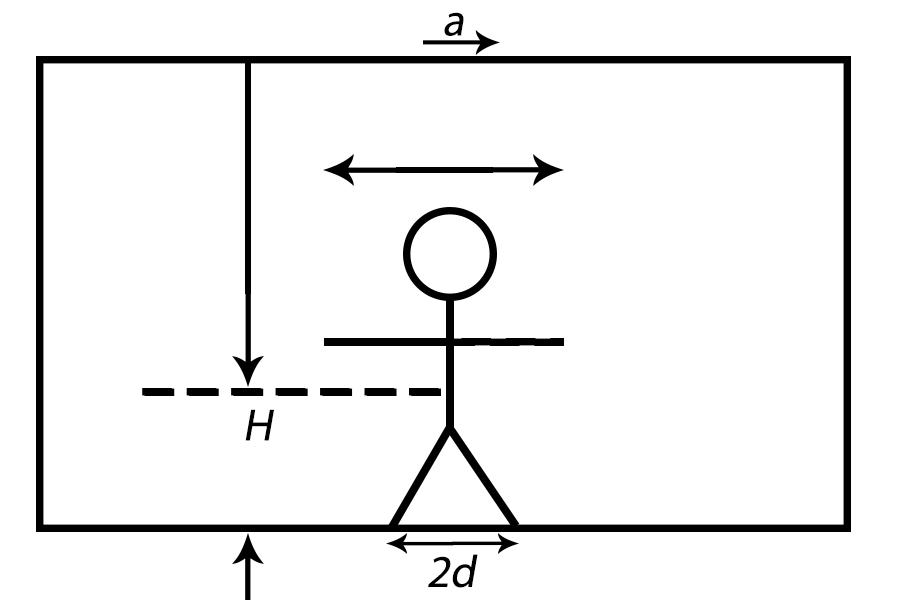
A. 2m(g+dHa);2m(g−dHa)
B. m(a+g);mg
C. dHma;2m(g−dHa)
D. mg;mg
Solution
The above problem can be resolved using the concept and applications of normal reactions, along with the fundamentals of the equilibrium of forces. In this problem, we suppose to balance the vertical component of force, that is the normal reaction acting on both foot. Moreover, the equilibrium is also applied to form some numerical equations, and these equations are then resolved using the substitution method, and this upon solving will provide the magnitude of normal reactions.
Complete step by step answer:
Given data:
The mass of body is, m.
The distance between the centre of mass and standing point is, H.
The distance between the legs is, 2d.
Apply the condition of the equilibrium of forces for the normal reaction force as,
N1+N2=mg…………………………………………. (1)
Here, N1 and N2 are the magnitude of normal reaction force on both the foot respectively and g the magnitude of gravitational acceleration.
The necessary condition of equilibrium for the given problem is,
maH=N1d−N2d…………………………………………. (2)
Modifying the above equation as,
