Question

A boy of mass M stands on a platform of radius R capable to rotate freely about its axis. The moment of inertia of the platform is I. The system is at rest. The friend of the boy throws a ball of mass m with a velocity v horizontally. The boy on the platform catches it. Find the angular velocity of the system in the process.
A) $\dfrac{{mvR}}{{\left( {M + m} \right){R^2}}}$
B) $\dfrac{{mvR}}{{I + M{R^2}}}$
C) $\dfrac{{mvR}}{{I + m{R^2}}}$
D) $\dfrac{{mvR}}{{I + \left( {M + m} \right){R^2}}}$

Answer 1

The platform starts rotating because the boys try to maintain the balance and frictional force comes into action. After looking at the system we can observe which quantity is conserved and then proceed accordingly.
Moment of Inertia is defined as the product of masses in the system and the square of the distance from the centre.

Complete step by step answer:
The system according to the question can be represented as:

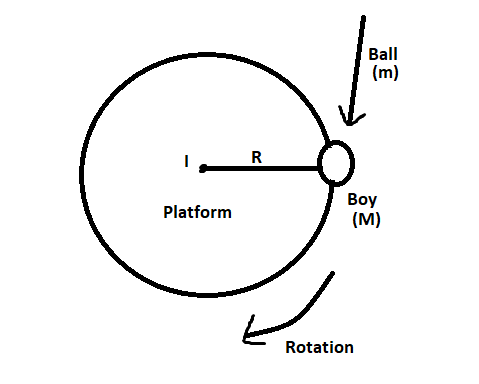
The net external torque is 0 (null) because all the forces acting upon the boy are internal. This implies that the angular momentum is conserved which is given as:
Initial angular momentum = Final angular momentum ________ (1)
Now,
Initial angular momentum = mvR [Product of linear momentum (mv) and distance from centre(R)]
Final angular momentum = Product of Moment of Inertia of the centre after the ball is catched (since the body starts rotating) and the angular speed $\left( \omega \right)$
Moment of Inertia at the centre = product of sum of masses and square of the distance from the centre.
Moment of Inertia of the centre = $[I + (M + m){R^2}]$
Thus, the final angular momentum = $[I + (M + m){R^2}]\omega$
Substituting these values of initial and final angular momentums in (1), we get:
mvR = $[I + (M + m){R^2}]\omega$
Calculating for angular speed $\left( \omega \right)$
$\omega = \dfrac{{mvR}}{{I + \left( {M + m} \right){R^2}}}$
Therefore, the angular velocity of the system in the complete given process is $\dfrac{{mvR}}{{I + \left( {M + m} \right){R^2}}}$, option D).

Note: Linear velocity (in line) is represented by ‘v’ where as angular velocity (in rotational motion) is represented by $'\omega '$ and the relationship is given as $v = \omega r$
Similarly,
Linear momentum is represented by p (p = mv) and angular momentum is denoted by Land the relationship is given as L = pr and thus L = mvr
r in both cases represents the distance of the object from the centre.