Question

A boy of length 10 m, to see his own complete image, requires a mirror of length at least equal to.
(A) $\dfrac{{10}}{4}$
(B) $\dfrac{{10}}{3}$
(C) $\dfrac{{10}}{2}$
(D) $10$

Answer 1

Hint
We proceed to solve this question by drawing a ray diagram of the boy standing in front of the mirror. Then compare the length of the boy to the length of the mirror using properties of reflection of light. Refer to the diagram in the complete solution for a better understanding.

Complete step by step answer

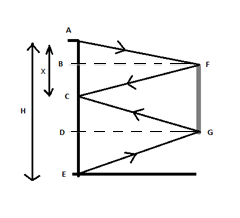
The line ABCDE represents the height of the boy. A is the top of the head, C is where the eyes are located and E is the feet. The light from the head as well as feet get reflected and reach the eyes to give vision.
Let us consider the length of the line ABCDE as $H$ and the length of the mirror as FG. FG is equal to the length of BCD.
Taking the distance AC as $X$ , we get the length of CE as $H-X$ .
$\angle AFB$ is equal to the angle $\angle BFC$ ( $\because$ angle of incidence is equal to the angle of reflection)
From this, we know that the length of AB and BC are the same and equal to $\dfrac{X}{2}$
Similarly, $\angle CGD$ and $\angle DGE$ are equal ( $\because$ angle of incidence is equal to the angle of reflection)
This tells us that line CD and DE are of the same length and equal to $\dfrac{H-X}{2}$
We know that the length of the mirror FG is equal to the sum of BC and CD. Length of mirror FG is equal to $\dfrac{{H - X}}{2} + \dfrac{X}{2} = \dfrac{H}{2}$
From the question, we know that the height of the boy is $10m$ . So, the minimum length of the mirror should be equal to $\dfrac{{10}}{2} = 5m$
Hence option (C) $\dfrac{{10}}{2} = 5m$ is the correct answer.

Note
This minimum length of the mirror required to see the entire body is regardless of the distance between the mirror and the object. The distance between the image and object is always twice the distance between the object and mirror.