Solveeit Logo
Login

Question

Question: A boy of height 1.5m with his eyes level at 1.4m stands before a plane mirror of length 0.75m fixed ...

A boy of height 1.5m with his eyes level at 1.4m stands before a plane mirror of length 0.75m fixed on the wall. The height of the lower edge of the mirror above the floor is 0.8m. then
A) The boy will see his full image
B) The boy cannot see his hair
C) The body cannot see his feet
D) The boy can see neither his hair nor his feet

Explanation

Solution

First we have to use the theorem for similar triangles. There are 3 triangles formed, the first triangle is formed at height 1.4m, second one is formed at height 0.8m, and then the third triangle has the height y. equate these triangle by using a theorem of similar triangle through this we have to find y. y is the length of image formed.

Complete Step by step solution:
Let y be the length of the image which can`t be seen by the boy.

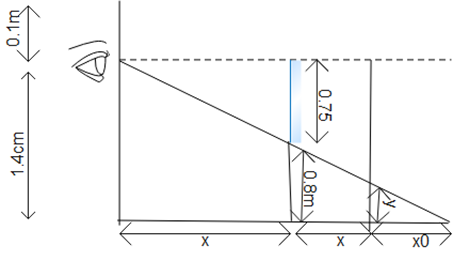
From, similar triangle theorem we get.
⇒yx0=0.8x+x0 ∴y=0.8×x0x+x0−−−−(1) \begin{aligned} & \Rightarrow \dfrac{y}{{{x_0}}} = \dfrac{{0.8}}{{x + {x_0}}} \\\ & \therefore y = \dfrac{{0.8 \times {x_0}}}{{x + {x_0}}} - - - - (1) \\\ \end{aligned}
Named above equation as (1)
Similarly, we get
1.4x+x+x0=0.8x+x0\dfrac{{1.4}}{{x + x + {x_0}}} = \dfrac{{0.8}}{{x + {x_0}}}
⇒1.4×(x+x0)=0.8×(2x+x0) ∴x0=x3 \begin{aligned} &\Rightarrow 1.4 \times \left( {x + {x_0}} \right) = 0.8 \times \left( {2x + {x_0}} \right) \\\ & \therefore {x_0} = \dfrac{x}{3} \ \end{aligned}
By rearranging the above equation we get
x=3×x0−−−−(2)x = 3 \times {x_0} - - - - (2)

Substitute equation (2) in equation (1) we get
⇒y=0.8×x03×x0+x0 ⇒y=0.8x04x0 \begin{aligned} & \Rightarrow y = \dfrac{{0.8 \times {x_0}}}{{3 \times {x_0} + {x_0}}} \\\ & \Rightarrow y = \dfrac{{0.8{x_0}}}{{4{x_0}}} \\\ \end{aligned}
∴y=0.2m\therefore y = 0.2m
Hence the length of the image he can't see in the mirror is 0.2m i.e he cannot see his feet.

So, option C is the correct answer.

Additional information:
A plane mirror is the mirror which has a flat reflective surface.
Plane mirrors produce virtual images.

Note:
We have basic knowledge, if the size of the mirror was 1.5m or greater than that then only a boy could have seen the image of full body.the minimum size of the mirror required to see his full image of the boy must have half of the boy size.