Question

A boy of $30\,kg$ balances a man of $60\,kg$ on a see-saw at a distance of $1.5\,m$ from the fulcrum. The distance of the man from the fulcrum is:
A. $1\,m$
B. $1.2\,m$
C. $0.75\,m$
D. $0.5\,m$

Answer 1

Here we have to use the theory of rotational equilibrium to get the answer. We have to balance the torques applied on both the weights.

Complete step by step answer:

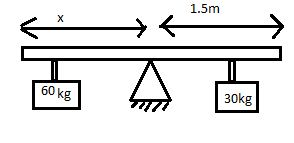
Given,
Weight of boy $= 30\,kg$
Weight of man $= 60\,kg$
Distance of the boy from the fulcrum $= 1.5\,m$
Let the distance of the man from the fulcrum be $x$
Now, we have to balance the torques to get the answer.
$60 \times gx = 1.5 \times 30g \\\ \Rightarrow 60gx - 1.5 \times 30g = 0 \\\ \Rightarrow x = 0.75\,m \\\$
Therefore, the distance of the man from the fulcrum is $0.75\,m$ .

So, the correct answer is “Option C”.

Additional Information:
Torque is a force measure that can cause an object to rotate around an axis. In linear kinematics, just as force is what causes an object to accelerate, torque is what causes an object to achieve angular acceleration. The torque vector orientation is dependent on the direction of the force on the axis.
In angular motion, torque is also known as the parallel of force. The tuning effect is thus algebraically strictly proportional to both the force magnitude and the perpendicular distance between the force vector and the hinge commonly referred to as the fulcrum in which angular motion is to take place.
For an unconfined object, or for a confined object, the product of the force and the perpendicular distance to the centre of gravity is referred to as the torque or moment.

Note:
The fulcrum lies in the middle of the body and the torque acts in the clockwise or anti-clockwise direction. So, the body is unbalanced. To balance the body we need to equate the torque on both sides.
Also we have to be careful while calculating the torques on both sides.