Question

A boy is standing on the ground and flying a kite with 100m of string at an elevation of ${{30}^{\circ }}$. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of ${{45}^{\circ }}$. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.

Answer 1

Hint: Draw the figure according to the description. The two kites from both boys should meet at a point. Consider a triangle with ${{30}^{\circ }}$ angle and find the height of the kite from the ground. Now take a triangle with ${{45}^{\circ }}$ angle and find the length of the kite using the sine function

Complete step-by-step answer:
It is said that a boy is standing on the ground. Let F be the boy. The kite is the point A at an elevation of ${{30}^{\circ }}$ from ground. Let BC be the roof of the building and B be the point where the ${{2}^{nd}}$ boy stands. The boy flies a kite at an elevation of ${{45}^{\circ }}$. The two kites meet at the point A. We need to find the length of string of the ${{2}^{nd}}$ boy which can be taken as the length of AB marked as ‘x’.

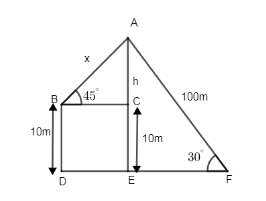
Let us consider AE as the height of kite from the ground DF. From the figure we can say that AC = h and CE = 10m. Take AE as H and AF = 100m.
$\angle AFE={{30}^{\circ }}$ and $\angle ABC={{45}^{\circ }}$, from the figure.
Let us consider $\Delta AFE$,
$\sin {{30}^{\circ }}$ = Opposite side / hypotenuse = $\dfrac{AE}{AF}=\dfrac{AC+CE}{AF}$.
From the trigonometric table we know that value of $\sin {{30}^{\circ }}=\dfrac{1}{2}$.
Put the value of AC = h, CE = 10m and AF = 100m.
$\dfrac{1}{2}=\dfrac{h+10}{100}$
Cross multiplying them,

& \Rightarrow h+10=\dfrac{100}{2} \\\ & h=50-10=40m \\\ \end{aligned}$$ Thus we got a value of h = 40m. Now let us consider $$\Delta ABC$$. $$\sin {{45}^{\circ }}$$ = Opposite side / hypotenuse = $$\dfrac{AC}{AB}=\dfrac{h}{x}$$. From the trigonometric table we know that, $$\sin {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$$ and put h = 40m. $$\therefore \dfrac{1}{\sqrt{2}}=\dfrac{40}{x}$$ Apply cross – multiplication property. $$x=40\sqrt{2}$$. $$\therefore $$ Length of the string = $$40\sqrt{2}$$. Hence we got the length of the string of the second boy as $$40\sqrt{2}$$m. Note: Be careful while drawing the figure, you miss a small detail or if it’s wrong, the entire answer will be wrong as it solely depends upon the figure. Sometimes, students do not understand what the question asks to find. So, they will end up finding the length of string as AF-AB. But, that is not needed as we have to find the length of string AB only and not the difference of the length of strings. Remember the trigonometric table values so it will be easy for you to solve.