Question
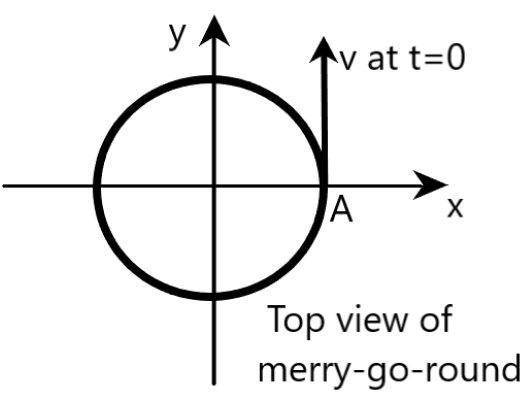
Question: A boy is sitting on the seat of a merry-go-round with a constant angular velocity. At \(t=0\), the b...
A boy is sitting on the seat of a merry-go-round with a constant angular velocity. At t=0, the body is at position A, as shown in the figure. Which of the following graphs are correct? All graphs are sinusoidal.
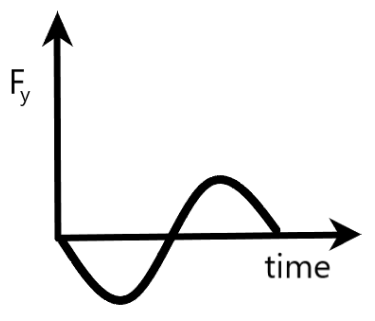
A)Fy is the y- component of the force keeping the boy moving in a circle
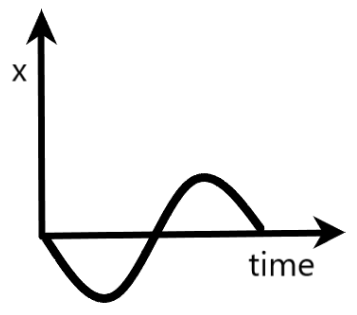
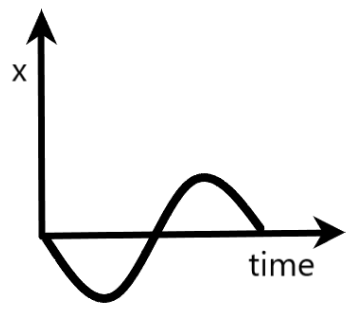
B)x is the x-component of the boy’s position
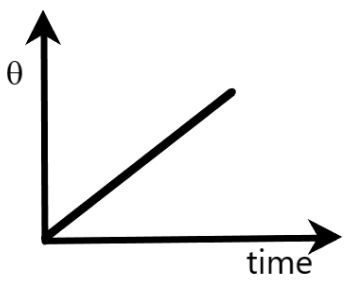
C)θ is the angle that the position vector of the boy makes with the positive x-axis
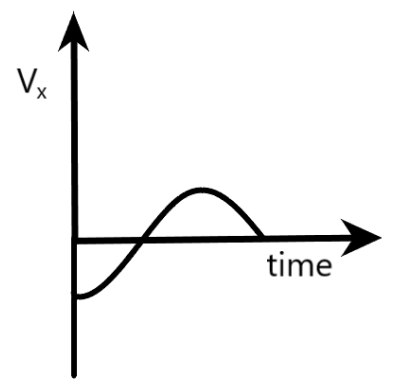
D)Vx is the x-component of the boy’s velocity
Solution
Each option is scrutinized by taking the position of the boy at a particular time t. When the boy moves from his initial position at t=0 to a position at time t, the angular displacement of the boy is taken as θ. Then, the required equations are derived and checked with the given graphs, one by one.
Complete step-by-step solution
We are given that a boy is sitting on the seat of a merry-go-round with a constant angular velocity. At t=0, the body is at position A. We are also provided with four graphs, which talks about different parameters with respect to the movement of boys in the merry-go-round. We are required to mark the correct graphs from these options.
For this, let us assume that the boy has already started moving in the merry-go-round and is at a position B now, as shown in the figures given below. Let t be the time at which the boy is at B, as shown.
Now, let us go through the provided options one by one.
A)Fy is the y- component of the force keeping the boy moving in a circle
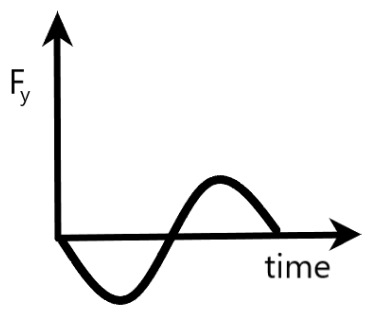
Here, we are told that Fy is the y- component of the force keeping the boy moving in a circle. From the graph, it is clear that Fy is in the form of a negative sinusoidal wave, moving with respect to time.
Now, let’s have a look at the figure given below.
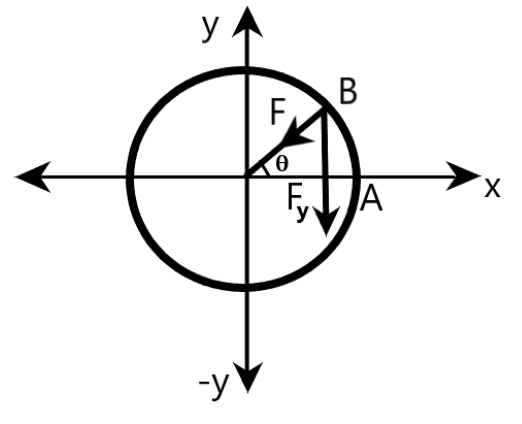
Clearly, the boy is at B, when the time is t. We know that force acting on the boy is the centripetal force, which is given by
F=mω2r
where
F is the centripetal force acting on the boy at time t
m is the mass of the boy
ω is the angular frequency of motion of the boy
r is the radius of the merry-go-round
Clearly, the centripetal force is acting along the position vector of the boy at B, as shown.
Now, the y-component of this centripetal force is given by
Fy=−mω2rsinθ=−mω2rsin(ωt)
where
Fy is the y-component of the centripetal force
θ=ωt is the angular displacement of the boy
Clearly, this component of force is acting along the negative y-direction
Also, if we draw a graph between Fy and t, it is of the form of a negative sine wave.
The graph given in option A satisfies this condition and hence, we can conclude that option A is correct.
B)x is the x-component of the boy’s position
x-component of the position vector of the boy at B can be deduced from the right triangle CEB, as shown below.
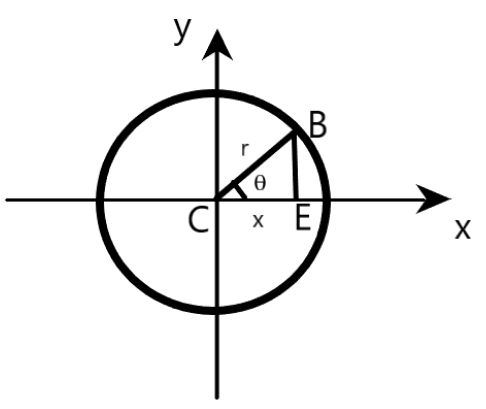
Clearly, x-component of the position vector of the boy at B is given by
x=rcosθ=rcos(ωt)
where
x is the x-component of the position vector of the boy at B
r is the radius of the merry-go-round
θ=ωt is the angular displacement of the motion of the boy
Now, if we draw a graph between x and t, it will have the shape of a cosine wave. Since the graph provided in the option is in the form of a sine wave, the given option is concluded as wrong.
C)θ is the angle that the position vector of the boy makes with the positive x-axis

We know that angular frequency is defined as angular displacement per unit time. If ω represents the angular frequency of the boy rotating in merry-go-round at time t, then, ω is given by
ω=tθ⇒θ=ωt
where
ω is the angular frequency of the boy at time t
θ is the angular displacement of the boy at time t
Clearly, angular displacement is directly proportional to time. Therefore, if we draw a graph between θ and t, it will look similar to the graph provided in the option, as given above.
Hence, option C is also correct.
D)Vx is the x-component of the boy’s velocity
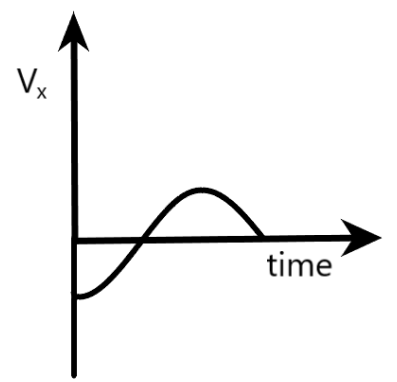
Here, we are said that Vx is the x-component of the boy’s velocity x-component of the velocity vector of the boy at B can be deduced from the right triangle CFB, where <B=θ, as shown below.
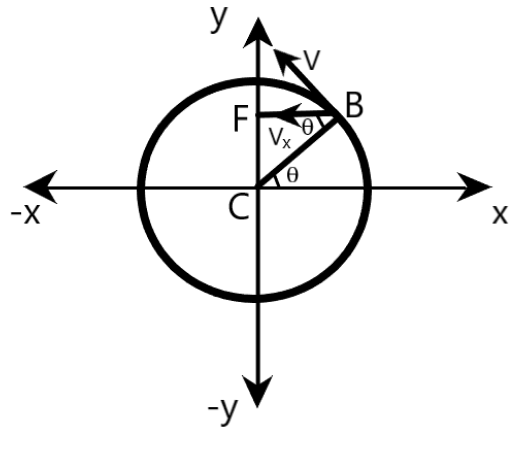
Here, the velocity of the boy at B is given by
V=ωr
where
V is the velocity of the boy at B
ω is the angular frequency of the motion of boy at time t
r is the radius of the merry-go-round
Clearly, this velocity is acting along the tangent drawn at B, as shown in the figure.
Now, the x-component of this velocity is given by
Vx=−ωrsinθ=−ωrsin(ωt)
where
Vx is the x-component velocity of the boy at B
θ=ωt is the angular displacement of the boy at t
Clearly, this component of velocity acts in the negative x-direction. If we draw a graph between Vx
and t, it will have the shape of a negative sine wave.
Since the provided option has the shape of a negative cosine wave, option D can be concluded as wrong.
Therefore, option A and option C is correct while option B and option D are incorrect for a boy moving in a merry-go-round.
Note: Such questions are asked to evaluate the visualizing capabilities of students. Therefore, students need to be thorough with the shapes of a positive sine wave, a negative sine wave, a positive cosine wave, and a negative cosine wave. Deducing the correct waveform from an equation is also important, which students should practice from time to time.
