Question

A boy and man carry a uniform rod of length L horizontally in such a way that the boy gets $\dfrac{1}{4}th$ of the rod. If the boy is at one end, the distance of the man from the other end is:
A.$\dfrac{L}{3}$
B.$\dfrac{L}{4}$
C.$\dfrac{{2L}}{3}$
D.$\dfrac{{3L}}{4}$

Answer 1

To determine the position of the man with respect to the rod, therefore the centre of mass of the rod and hence the torque acting on the rod are to be determined. Given that the mass of the rod is uniformly distributed so the load can be considered to be acting at its center of gravity.

Complete answer:
Step I:
Let X be the distance of the man from the center of the rod. It is given that the boy gets$\dfrac{1}{4}th$ of the rod, therefore, if the total weight is W, then weight supported by the boy will be $\dfrac{W}{4}$ .

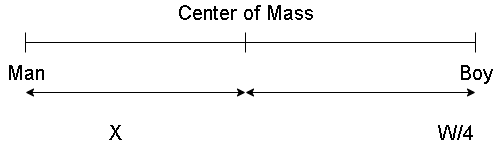
Let ‘L’ be the length of the rod and since the load is uniformly distributed at center of mass, the distance of boy from the center of the rod will be $\dfrac{L}{2}$ and let ‘X’ be the distance of man from the other end of the rod.
Step II:
Since the rod is acting in a horizontal position, therefore the net torque acting on the rod will be zero.
If W is the weight, then load supported by man will be

$$ Total weight of the rod – Load supported by the boy Or $W - \dfrac{W}{4} = \dfrac{{3W}}{4}$ ${F_{man}} = \dfrac{{3W}}{4}$ ${F_{boy}} = \dfrac{W}{4}$ Step III: In case of rotational equilibrium, the net torque acting on the object will be equal to zero. This means there is no net torque acting on the rod. In that case, Force applied by the boy = Force applied by the man $\dfrac{W}{4} \times \dfrac{L}{2} = \dfrac{{3W}}{4} \times X$ $X = \dfrac{{W \times L \times 4}}{{4 \times 2 \times 3W}}$ $X = \dfrac{L}{6}$ Step IV: Distance of man from the other end is$\dfrac{L}{2} - X = \dfrac{L}{2} - \dfrac{L}{6}$ Or Distance of man from the other end is $\dfrac{L}{3}$ **Option A is the right answer.** Note:** Center of mass is a position or a point at which the whole mass of the body is said to be concentrated. It is the average position of all the parts of the system or a body. Also when there is no movement of the object or if it is moving with a constant angular velocity, it is said to be in rotational equilibrium.