Question

A boy 1.54 m tall can just see the sun over a wall 3.64 high which is 2.1 m away from him. Find the angle of elevation of the sun.

Answer 1

In this we will find angle of elevation by using trigonometry. Since the height of the wall and how far the boy is standing is given i.e. if all the circumstances form a triangle then the length of opposite side and the length of the adjacent side is given. Hence by using $\tan \theta$ we will find the angle of elevation.

Complete step-by-step answer:
The figure of given condition is given below.

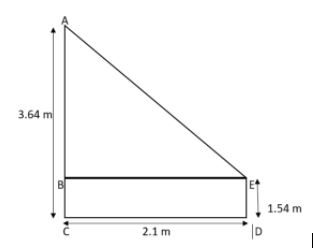
In figure the side ED represents the boy, side AC represents the wall and the side CD represents the distance of the boy from the wall.
Given that length of side AC = 3.64 m,
length of side CD = 2.1 m,
length of side DE = 1.54 m.
Since BC is parallel to ED and CD is parallel to BE.
Length of side BE = 2.1 m and length of side DE = 1.54 m .
Since boy view sun from point E. Hence will find tangent angle at point E.
$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$
Opposite side = side AB
Length side AB = length of side AC – length of side BC
Length side AB = 3.64 – 1.54.
Length side AB = 2.10.
$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$
$\tan \theta =\dfrac{\text{length of AB}}{\text{length of BE}}$
$\tan \theta =\dfrac{2.1}{2.1}$
$\tan \theta =1$
$\theta ={{\tan }^{-1}}1$
$\theta =\dfrac{\pi }{4}$
Hence, the angle of elevation is $\theta =\dfrac{\pi }{4}$.

Note: In this problem one should note that we did not calculate the angle from the foot of the boy. As he is looking at the sun when he is standing. Also, the student should know what is sine, cosine and tangent when we use the trigonometric function to find the length of one side and the angle between the sides of the triangle and what is the inverses of trigonometric functions.