Question

A boy $1.4$ m tall casts a shadow $1.2$ m long at the time when a building casts a shadow $5.4$ m long. Find the height of the building.
A) $6.3$
B) $4.8$
C) $7.2$
D) $8.0$

Answer 1

The given problem contains heights of two different objects and they are compared in the same set of units. We will use the simple comparison of the ratios and determine the required quantity by simply rearranging the terms in the equation obtained from the basic given conditions.

Complete step-by-step solution:
Note that the given quantities are in the same unit so we need not have to change any units before solving the problem.
The height of the given boy is $1.4$ m.
The same boy with the given height casts a shadow of the height $1.2$ m.
The height of the shadow cast by the building is $5.4$ m.

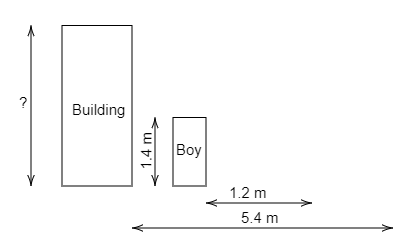
We need to find the height of the building.
Let us assume that the height of the building is $x$ m.
Since all the shadows are cast at the same time, the height of the shadows will be proportional to the height of the respective objects.
Therefore, we can write the following equation for the proportion:
$\dfrac{x}{{1.4}} = \dfrac{{5.4}}{{1.2}}$
Rearrange the terms to find the value of $x$ .
$x = \dfrac{{5.4 \times 1.4}}{{1.2}}$
Simplify the right-hand side to write,
$x = 6.3$
Therefore, the height of the building is $6.3$ m.

Thus, the correct answer is A.

Note: Even though the given problem contains shadow and the heights it is not a trigonometry problem as there is no any angle given in the example. Second of all the proportion is easy to see as the timing for the shadow is the same. Rearrange the terms properly and just simplify correctly to solve the given problem.