Question

A box weighing 2000 N is to be slowly slid through 20 m on a straight track having friction coefficient 0.2 with the box. Find the work done by the person pulling the box with a chain at an angle θ with the horizontal.

Answer 1

For just sliding the box without any acceleration force applied on the box will be just enough to counterbalance the frictional force provided by the floor.
Apply the equilibrium conditions:
$\sum {{F_x} = 0,\sum {{F_Y} = 0} }$
Then, find the work done by the expression,
Work done = component of force acting in the direction of displacement $\times$ total displacement of the box

Complete step by step answer:
Let’s start with a free body diagram.

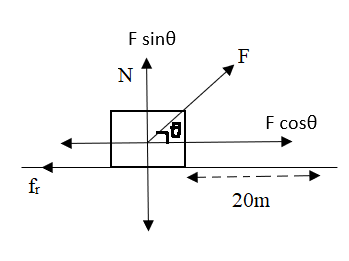
Given that,
Weight of the box = 2000 N
Friction coefficient $= \mu = 0.2$
The box slowly slid through the floor about 20 m.
From free body diagram the forces acting on the boxes are:
Weight of the box is acting downwards,
W = mg = 2000 N
Normal reaction force will be acting upwards.
The force exerted by a person will have two components given by $Fcos\theta$ and $Fsin\theta$.
The frictional force acting on the box $= {f_r} = \mu N$
To make the box to remain in its equilibrium condition, the sum of all forces acting on the box is zero.
Thus, on applying equilibrium conditions.
$\sum {{F_y} = 0}$ (forces acting in vertical direction)
$\Rightarrow N + F\sin \theta - 2000 = 0$
$\Rightarrow N = 2000 - F\sin \theta$
Similarly,
$\sum {{F_x} = 0}$
$\Rightarrow F\cos \theta - {f_r} = 0$
$\Rightarrow F\cos \theta = {f_r}$
$\Rightarrow F\cos \theta = \mu N = 0.2N$
Substituting, the value of normal force N, we get
$\Rightarrow F\cos \theta = 0.2(2000 - F\sin \theta )$
$\Rightarrow F\cos \theta + 0.2F\sin \theta = 400$
$\Rightarrow F = \dfrac{{400}}{{\cos \theta + 0.2\sin \theta }}$
Therefore, work done in pushing the block is given by
$\Rightarrow W = F.s$
$\Rightarrow W = F\cos \theta \times s$
$\Rightarrow W = 20\left( {\dfrac{{400}}{{\cos \theta + 0.2\sin \theta }}} \right)\cos \theta$
$\Rightarrow W = \dfrac{{8000}}{{1 + 0.2\tan \theta }}joule$

Note:
The formula for work done is given by a dot product, hence it is a scalar quantity. Mathematically it is given by $W = \vec F.\vec s$
The SI unit of work is joule(J).