Question

A box is dragged across a floor by a rope which makes an angle of ${45^ \circ }$ with the horizontal. The tension in the rope is 100 N, while the box is dragged 10 m. The work done is
A. 607.1 J
B. 707.1 J
C. 1414.2 J
D. 900 J

Answer 1

Resolve the tension in the rope in vertical and horizontal components. Now find out which component of the tension (force applied) contributes to the work done i.e. angle between force and displacement. Use the formula:
$W = \overrightarrow F .\overrightarrow {ds} = \left| {\overrightarrow F } \right|\left| {\overrightarrow {ds} } \right|\cos \theta$

Complete step by step answer:

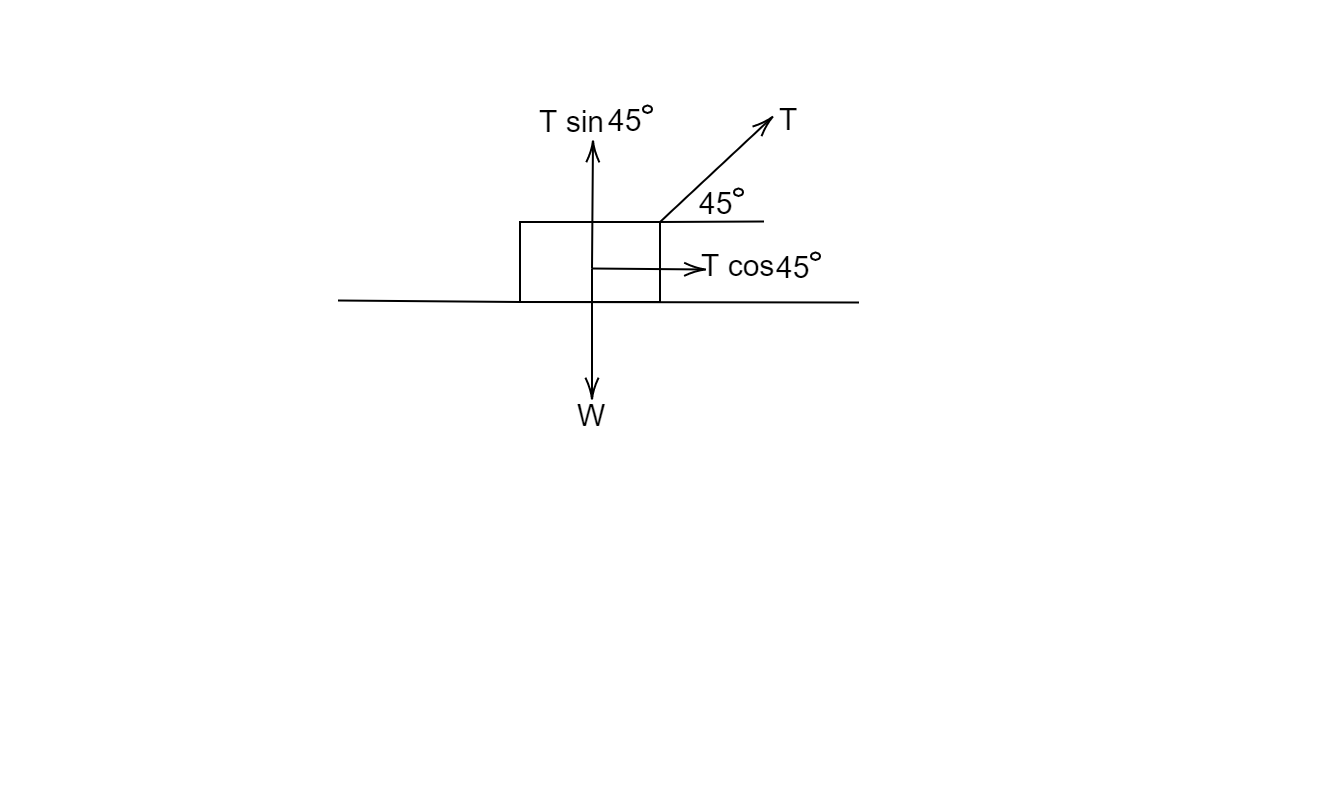
From the given data we have resolved the tension in the string into two components. The vertical component (Normal Reaction Force) balances out the weight of the box. The horizontal force is responsible for the motion of the box.
The angle between the normal reaction force and displacement is $90^\circ$ therefore by the formula,
$W = \overrightarrow F .\overrightarrow {ds} = \left| {\overrightarrow F } \right|\left| {\overrightarrow {ds} } \right|\cos \theta$
$W = 0$
The work done by the horizontal force is,
$W = (100\cos {45^ \circ })(10)\cos {0^ \circ } \\\ W = \dfrac{{1000}}{{\sqrt 2 }} = 707.1J \\\$
Hence the total work done is $707.1J$.

So, the correct answer is “Option B”.

Additional Information:
If frictional force was also given then, the total work done = work done by the person – work done by the frictional force,
Where, frictional force ${f_s} = \mu {\rm N} = \mu mg$ .

Note:
The tension is equal and opposite in direction to the force applied F. Therefore, instead of F, the use of tension T has been done in the problem. Also, work done is a scalar quantity. So, be careful in the questions involving force and displacement vector equations.