Question

A box has two compartments of equal volume separated by a divider each compartment filled with a random sample of n moles of a certain gas, but the pressure in compartment A is twice the pressure in compartment B. Identify which of the following statements is true?

Answer 1

Using the Gay Lussac's law which states that if the volume is kept or is in a constant state, then the pressure of the gas changes with the change in the temperature of the gas. The condition can be mathematically written as:
$\dfrac{P}{T}=k$
where P is the pressure of the given mass of gas, T is the temperature and k is the value of constant.

Complete step by step answer:
According to the situation given in the question there is a box divided into two volumes. The number of moles of gas filled in each compartment is n.
The pressure in compartment A is taken as 2P
The pressure in compartment B is taken as P.
Now the below graph represents the relationship between pressure and temperature when performing in accordance to the Gay Lussac’s Law:

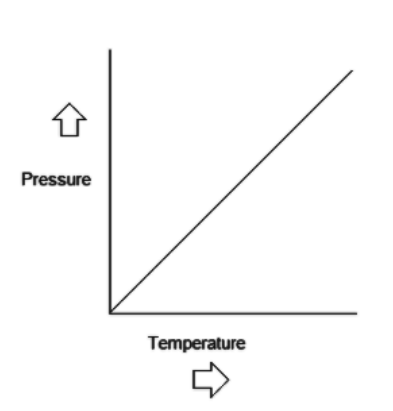
Now according to Gay Lussac's law the only parameters that we need in such situation are temperature, pressure and volume or like given here number of moles will do as well. Hence, option C and E which states gas constant and isotopes are rejected due to non-functionality and unnecessary clauses. Now let us focus on options A, B and D.
With Gay Lussac's Law in mind, we can say that we can say that if the pressure is doubled, the temperature is also doubled and the temperature is influenced by pressure and not by temperature of the other compartment hence, increasing four times is not possible.

Hence, the correct answer is option (A).

Note: Similarly if the pressure of the gas can influence the temperature so does the temperature of the gas can back influence the pressure as well. The formula for a two portion exchange of pressure and temperature is given as:
${{P}_{1}}{{T}_{1}}\text{ }=\text{ }{{P}_{2}}{{T}_{2}}$