Question
Question: A box contains 3 coins: Coin A: Fair coin (head probability) = $\frac{1}{2}$. Coin B: Biased coin ...
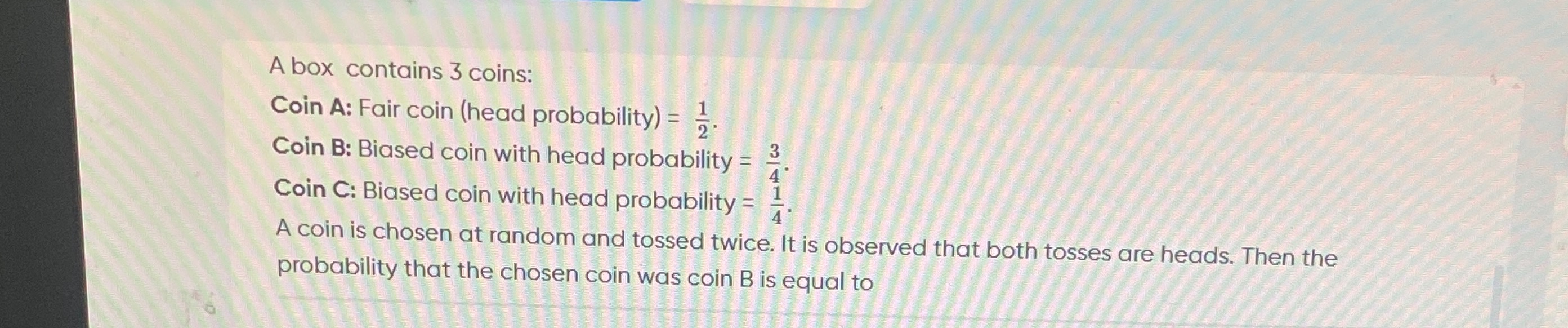
A box contains 3 coins:
Coin A: Fair coin (head probability) = 21.
Coin B: Biased coin with head probability = 43.
Coin C: Biased coin with head probability = 41.
A coin is chosen at random and tossed twice. It is observed that both tosses are heads. Then the probability that the chosen coin was coin B is equal to
A
149
B
31
C
247
D
169
Answer
149
Explanation
Solution
- Probabilities of choosing coins: Since a coin is chosen at random, the prior probabilities are equal: P(CA)=P(CB)=P(CC)=31.
- Probabilities of observing two heads (HH) given the chosen coin:
- Coin A (Fair): P(HH∣CA)=(21)2=41.
- Coin B (Biased): P(HH∣CB)=(43)2=169.
- Coin C (Biased): P(HH∣CC)=(41)2=161.
- Apply Bayes' Theorem: We want to find the posterior probability P(CB∣HH). Bayes' Theorem states: P(CB∣HH)=P(HH)P(HH∣CB)P(CB) The probability of observing two heads, P(HH), is calculated using the law of total probability: P(HH)=P(HH∣CA)P(CA)+P(HH∣CB)P(CB)+P(HH∣CC)P(CC)
- Substitute values and calculate: P(HH)=(41)(31)+(169)(31)+(161)(31) P(HH)=31(41+169+161)=31(164+169+161)=31(1614)=31(87)=247 Now, substitute this into Bayes' Theorem: P(CB∣HH)=247(169)(31)=247489=489×724=2×79=149
