Question

A bottle has an opening of radius a and length b. A cork of length b and radius $\left( {a + \Delta a} \right)$ where $\left( {\Delta a < < a} \right)$ is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and the frictional coefficient between the bottle and cork is $\mu$ then the force needed to push the cork into the bottle is:

A. $\left( {\pi \mu Bb} \right)a$
B. $\left( {2\pi \mu Bb} \right)\Delta a$
C. $\left( {\pi \mu Bb} \right)\Delta a$
D. $\left( {4\pi \mu Bb} \right)\Delta a$

Answer 1

In order to find the solution of the given question first we will find the force which is acting on the surface in the opposite direction of the cork, then we will find the value of stress and after substituting all the values in the equation of force we will find the required force needed to push the cork into the bottle.
Formula Used: $B = \dfrac{{Stress}}{{Strain}}$

Complete step by step answer:

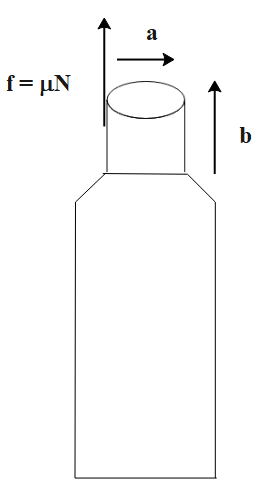
Force acting on the surface against the direction of the force by cork is given by,
$f = \mu N$ -(1)
Where ‘f’ is the force, ‘$\mu$’ is the frictional coefficient between the bottle and cork and ‘N’ is the normal force.
Since, we know that,
Stress $= \dfrac{N}{A} = \dfrac{N}{{\left( {2\pi a \times b} \right)}}$
$\Rightarrow B = \dfrac{{Stress}}{{Strain}}$
Here, ‘B’ denotes the bulk modulus of the cork.
$\Rightarrow Stress = B \times Strain$
Now, substituting the values we get,
$\Rightarrow \dfrac{N}{{2\pi ab}} = B \times \dfrac{{2\pi a \times \Delta a \times b}}{{2\pi {a^2} \times b}}$
$\Rightarrow N = B \times \dfrac{{4{\pi ^2}{a^2}b \times \Delta a}}{{2\pi {a^2}}}$
$\Rightarrow N = B \times 4\pi b \times \Delta a$
So, $N = 4\pi \Delta abB$
Substituting the value of ‘N’ in equation (1) we will get,
$\therefore f = \mu N = \left( {4\pi bB\mu } \right)\Delta a$
Thus, the force needed to push the cork into the bottle is $\left( {4\pi bB\mu } \right)\Delta a$.

Hence, option (D) is the correct answer.

Note :
Modulus of elasticity is defined as the measure of the ability of an object or a body to resist deformation. Mathematically, it is given as the ratio of stress and strain. Young’s modulus is a mechanical property of a solid material that measures the stiffness of that material. It is defined as the relationship between stress i.e. force per unit area and strain i.e. proportional deformation in a material in the linear elasticity regime of a uniaxial deformation. Young’s modulus is derived from Hooke’s law for small deformations i.e. when the deformation is small, the stress in the body is proportional to the corresponding strain.