Question
Question: A bomber is flying horizontally with a constant speed of \(150\;m/s\) at a height of \(78.4\;m\). Th...
A bomber is flying horizontally with a constant speed of 150m/s at a height of 78.4m. The pilot has to drop a bomb at an energy target. At what horizontal distance from the target should be releasing the bomb.
A. Zero
B. 300 m
C. 600 m
D. 750 m
Solution
Here, we use the concept of projectile motion which is fired horizontally from a certain height having a parabolic path. If an object is thrown with an initial velocity and which is then allowed to move under the action of gravity alone is called a projectile. Also, the path followed by a projectile during its flight is called a trajectory.
Complete step by step answer:
According to this question, when a bomb is dropped by the pilot to hit the target, the velocity of the bomb is unaffected by the vertical acceleration and its initial velocity becomes zero.
A bomb can be drop at certain height (h) =78.4m
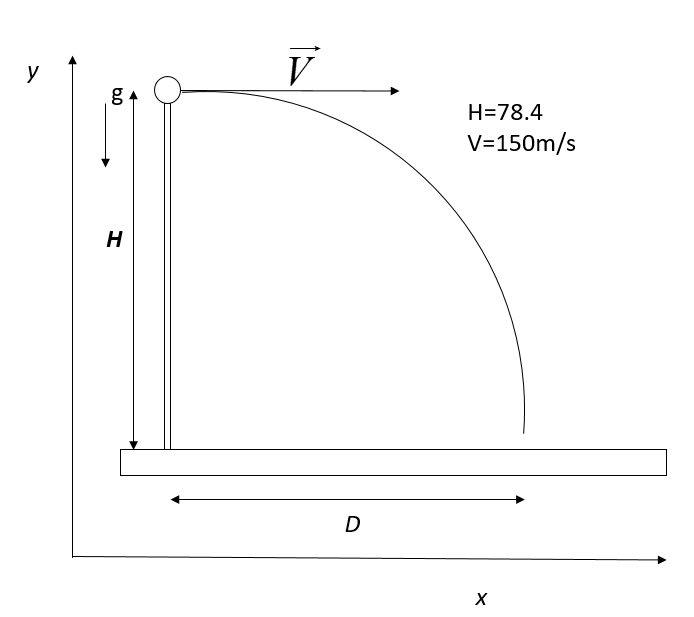
So, the time (T) of flight for bomb T=g2h
∴T=9.82×78.4=16=4s
Where g is gravity =9.8m/s
Now we find the horizontal distance from the target when the bomb is released.
So, the horizontal range in projectile motion R=u×T
Where T is the time of flight, and u is the initial velocity given =150m/s
∴R=150m/s×4s=600m
Therefore the bomb is released 600m away from the target. Hence the correct option is (C).
Note:
Since in this problem, the motion is regarding the projectile and if we were asked to calculate the maximum range of a projectile then we can determine it by using the formula,
Formula used: R=gu2sin2θ
Here R is the range, g is the acceleration due to gravity, u is the initial velocity, θ is the angle of projection.
When θ=45∘ ,
⇒Rmax=gu2
