Question

A bomb of mass $3m$ is kept inside a closed box of mass $3m$ and length $4L$ at its centre. It explodes in two parts of mass $m$ and $2m$. The two parts move in the opposite directions and stick to the wall of the box. The box is kept on a smooth horizontal surface. What is the distance moved by the box during this time interval.

& A.0 \\\ & B.\dfrac{L}{6} \\\ & C.\dfrac{L}{12} \\\ & D.\dfrac{L}{3} \\\ \end{aligned}$$

Answer 1

Hint: since the energy of the system is conserved. We can calculate the momentum of the system before explosion using the centre of mass of the system must be equal to the momentum after explosion. When equating, we can get the displacement due to explosion.

Formula used: $x_{cm}=\dfrac{m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}}{m_{1}+m_{2}+m_{3}}$

Complete step-by-step answer:
Initially when the bomb–box system is at rest, the centre of mass of the system is at the middle of the system. When the bomb explodes, the mass gets divided into $m,2m$and gets stuck to the opposite walls of the box, then the centre of the box gets displaced. Assume that the system moves by a distance $x$.
Since there is no external force acting on the system, the centre of the system remains the same. From the conservation of energy we know that energy of the system is conserved.
Then using, the equation for centre of mass, we know that:$x_{cm}=\dfrac{m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}}{m_{1}+m_{2}+m_{3}}$
When the bomb explodes,$m_{1}=m$ and $m_{2}=2m$, also the mass of the box$m_{3}=3m$
Since the centre of mass of the system doesn't change, $x_{cm}=0$and the total mass of the system is$m_{1}+m_{2}+m_{3}=6m$.

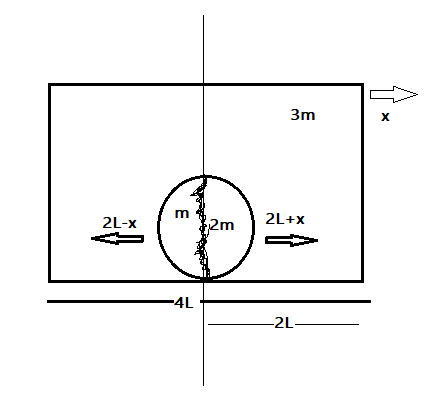
If $m_{3}$ moves $x$ towards the right , $m_{1}$ moves $2L-x$ towards left, and $m_{2}$ moves $2l+x$ towards right, using sign conventions, with respect to the centre of the system, taking towards right as positive and towards left as negative, we have.
Then ,$m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}=0$
$-m(2L-x)+2m(2L+x)+3m(x)=0$
$-2Lm+mx+4Lm+2mx+3mx=0$
Taking all the $Lm$ terms to one side, we get
$2Lm=-6mx$
$x=\dfrac{-L}{3}$
i.e. the box moves $\dfrac{L}{3}$ towards the left.
Hence the answer is D. $\dfrac{L}{3}$

Note: When taking the sign convention, it is better to take it with respect to the centre of the system, for easy calculation. Also pay attention to the sign convention and the final answer. If the answer is negative, then we must change the direction in which the system moves after explosion as shown here. Also, since there is no external force on the system, $x_{cm}=0$.