Question

A body thrown vertically up to reach its maximum height in $t$ second. The total time from the time of projection to reach a point at half of its maximum height while returning (in second) in
A) $\sqrt 2 t$
B) $1 + \dfrac{1}{{\sqrt 2 }}t$
C) $\dfrac{3}{2}t$
D) $\dfrac{t}{{\sqrt 2 }}$

Answer 1

The time taken to reach maximum height is equal to the time taken to reach to the earth as drag due to air is not considered while solving the projectile equations. Also, the horizontal acceleration is zero the only acceleration is in a vertical direction and which is the acceleration due to gravity. The acceleration for vertical motion will be acceleration due to gravity with a proper sign which is decided by the direction of motion of the body.

Formula used:
The formula of the Newton’s law of motion is $v = u + at$ and ${v^2} = {u^2} + 2as$ where $v$ is the final velocity, $u$ is initial velocity, $a$ is acceleration, $t$ is time and s is displacement.

Complete step by step answer:

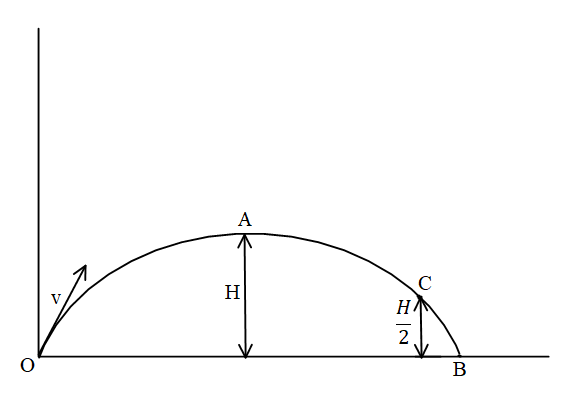
For the vertical motion, the time taken to reach maximum height is $H$ is,
${v_A}^2 = {v_o}^2 - 2gH$
As the final velocity is zero at maximum height.
$\Rightarrow 0 = {v_o}^2 - 2gH$
$\Rightarrow {v_o} = \sqrt {2gH}$………eq. (1)
$\Rightarrow {v_A} = {v_o} + at$
$\Rightarrow 0 = {v_o} - gt$
$\Rightarrow t = \dfrac{{{v_o}}}{g}$………eq. (2)
Replace the value of ${v_o}$ from equation (1) to equation (2).
$t = \dfrac{{{v_o}}}{g}$
$\Rightarrow t = \dfrac{{\sqrt {2gH} }}{g}$
$\Rightarrow t = \sqrt {\dfrac{{2H}}{g}}$………eq. (3)
Applying the relation for the motion from the point A and C.
${v^2} = {u^2} + 2as$
$\Rightarrow {v_C}^2 = {v_A}^2 + 2as$
$\Rightarrow {v_C}^2 = 0 + 2g\left( {\dfrac{H}{2}} \right)$
$\Rightarrow {v_C}^2 = 0 + gH$
$\Rightarrow {v_C} = \sqrt {gH}$………………….…eq. (4)
For the motion from A to C.
${v_C} = {v_A} + a{t_1}$
$\Rightarrow {v_C} = 0 + g{t_1}$
$\Rightarrow {v_C} = g{t_1}$…………………...……eq. (5)
Replace the value of ${v_C}$ from the equation (5).
$\Rightarrow {v_C} = g{t_1}$
$\Rightarrow \sqrt {gH} = g{t_1}$
$\Rightarrow {t_1} = \sqrt {\dfrac{H}{g}}$………………………...eq. (6)
Comparing equation (1) and (6).
${t_1} = \dfrac{t}{{\sqrt 2 }}$……………...……eq. (7)
So the time taken to half of the maximum height while returning is equal to,
$\Rightarrow {t_2} = t + {t_1}$
$\Rightarrow {t_2} = t + \dfrac{t}{{\sqrt 2 }}$ (Replace the value of ${t_1}$from equation (7))
$\Rightarrow {t_2} = t\left( {1 + \dfrac{1}{{\sqrt 2 }}} \right)$

Hence the correct answer is option B.

Note:
The sign of acceleration due to gravity is positive only if the motion is in the direction of acceleration due to gravity and the sign is negative if the motion is in the opposite direction of acceleration due to gravity.