Question

A body that starts from rest accelerates uniformly along a straight line at the rate of $10{\text{ }}m{s^{ - 2}}$ for $5\sec$ . It moves for $2\sec$ with a uniform velocity of $50{\text{ }}m{s^{ - 1}}$ . Then it retards uniformly and comes to rest in $3\sec$ . Draw the velocity-time graph of the body and find the total distance travelled by the body.

Answer 1

The distance travelled is shown by the area under the speed-time graph. For the motion of a particle, distance-time graphs and acceleration-time graphs can be produced, with time always displayed on the horizontal axis. A particle with a constant speed is represented by a straight line on a distance-time graph.

Complete step by step answer:
Let us first write the given values
Acceleration $\left( a \right) = 10\,m{s^{ - 2}}$
Time $\left( t \right)$ is given as $5\sec$
Therefore the velocity can be found by using equation of motion that is given by:
$v = u + at \\\ \Rightarrow v = 0 + 10 \times 5 \\\ \Rightarrow v = 50m{s^{ - 1}} \\\$
Now, it moves for $2$ seconds with a uniform velocity of $50{\text{ }}m{s^{ - 1}}$ and finally gets retarded to rest in $3\sec$.Using the above information we will draw velocity time graph accordingly;

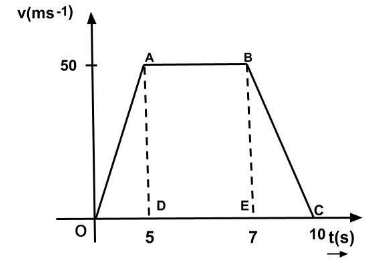
Now, according to the graph: the total distance travelled is $\left( D \right)$ = Area under the curve. Therefore,
$D = \dfrac{1}{2} \times \left( {OC + AB} \right) \times AD$
$\Rightarrow D = \dfrac{1}{2} \times \left( {10 + 2} \right) \times 50 \\\ \Rightarrow D = \dfrac{1}{2} \times 12 \times 50 \\\ \therefore D = 300\,m \\\$
Hence, the total distance travelled by the body is $300\,m$.

Note: It's important to remember that finding the area doesn't fully describe displacement because, being a vector quantity, displacement also requires a direction.Finding the location simply provides a number, not a direction. The magnitude of the displacement, which is equivalent to the distance travelled, is represented by the area under the curve (only for constant acceleration).