Question

A body starts to slide over a horizontal surface with an initial velocity of a $1m/s$. Due to friction, its velocity decreases at the same rate of $0.1m/{s^2}$ .How much time will it take for the body to stop?

Answer 1

Hint - To solve this problem, firstly we will learn about motion, laws of motion and the equations of motion, by using the concept behind them and its relation with our question, use the appropriate formula to find the required values, and by using this information we will easily approach our answer.

Step-By-Step answer:
It is defined as the change of position of an object with respect to time. Example- A book falling off a table, water flowing from the tap, rattling windows, etc. Motion is described in terms of the following terms. Distance, Displacement
Both distance and displacement are used to trace the change in position. Displacement is nothing but the shortest distance between the two distinct points. Displacement is measured as the shortest distance between the initial and final position.
Newton’s Laws of Motion
The first law, also called the law of inertia, every object in a state of uniform motion will remain in that state of motion unless an external force acts on it.
Second law of motion states that force equals the product of mass acceleration.
Third law of motion states that, for every action there is$=$ and opposite reactions.
Equations of Motion- Three equations of motion which describe the relationship between velocity, time, acceleration and displacement.
First equation of motion is:
$v = u + at$
Second equation of motion is:
$S = ut + \dfrac{1}{2}{a^2}$
Third equation of motion is:
${v^2} = {u^2} + 2aS$

Given,
$u = 1$
$a = - 0.1$
$v = 0$
By first equation of motion, we have
$v = u + at$
$0 = 1 - 0.1 \times t$
$t = 10\sec$

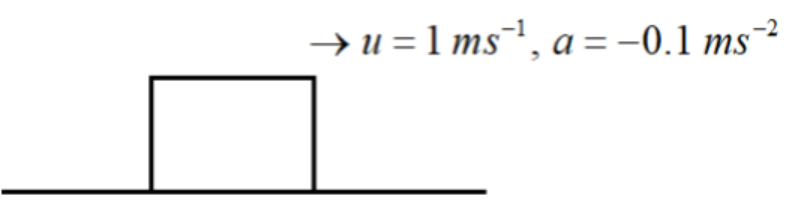
Note - The first equation of motion deals with final velocity, initial velocity, acceleration and time. We can use the first equation of motion to find final velocity, initial velocity, acceleration and time.