Question
Question: A body starts from rest and travels a distance S with uniform acceleration, then moves uniformly a d...
A body starts from rest and travels a distance S with uniform acceleration, then moves uniformly a distance 2S and finally comes to rest after moving further 5S under uniform retardation. The ratio of the average velocity to maximum velocity is
(a) 2/5
(b) 3/5
(c) 4/7
(d) 5/7
Solution
Use the concept of Motion In A Straight Line. Area of triangle= 21×base×height and Area of rectangle = base×height.
Complete step by step solution:
Area of the (V–t) curve represents displacement.
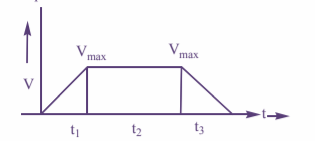
S=21vmaxt1⇒t1=vmax2S 2S=21vmaxt2⇒t2=vmax2S 5S=21vmaxt2⇒t3=vmax10S
Vavg=Total timeTotal displacement vmax2S+vmax2S+vmax10SS+2S+5S=(vmax14S)8S=vmax74
The ratio of the average velocity to maximum velocity= vmaxvavg=vmaxvmax74=74
Correct Answer: (c) 4/7
Note: Alternative Method-
vmaxvavg=2(Total displacement during acceleration and retardation) + (Displacement During uniform velocity)Total displacement
∴vmaxvavg=2(S+5S)+2S8S=148=74
