Question

A body rolling down a hill has:
A. K.E. only
B. P.E. only
C. Neither K.E. nor P.E.
D. Both K.E. and P.E.

Answer 1

When a body rolls down a hill it has two types of motion. it has a translation motion as well as it has a rotational motion when a body moves it has a kinetic energy so you can observe which type of energy has a rolling body.

Complete step by step answer:
Let’s take an example to understand this question: we take a sphere rolling down from a hill or an inclined plane of height $h$. When it rolls down at that time it has two types of motion one is translation motion.

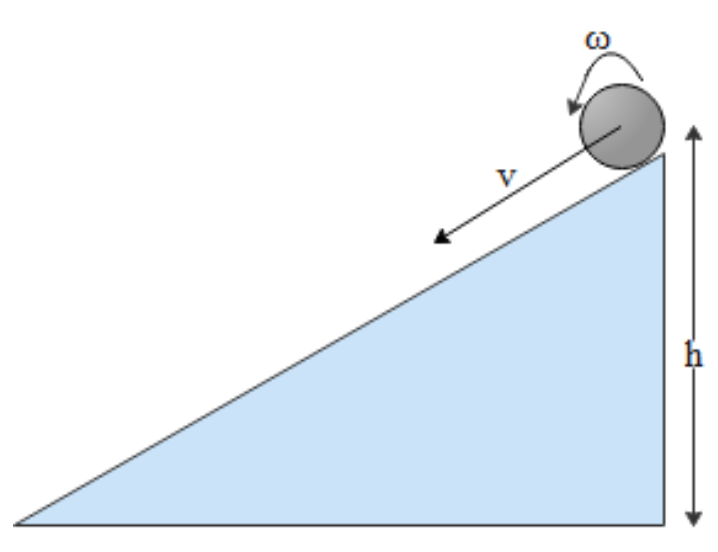
A body rotating about the centre of mass with an angular velocity $\omega$ as well as the body has a translation motion with a velocity $v$ means this body has two velocities it means it also has a kinetic energy.
And as we know when a body situated at $h$ height from ground it has a potential energy due to gravitation of earth. This is equal to $mgh$
So it is clear that when a body rolls down from a hill it has both types of energy kinetic energy as well as potential energy.
When a ball is rolling from the hilltop, the potential energy will decrease and kinetic energy will increase until it reaches the ground.

So, the correct answer is “Option D”.

Note:
Some time student get confused which type of kinetic energy has a rolling body as it is clear when a body roll down is move with a translation velocity $v$ as well as an angular velocity $\omega$ so it has two types of kinetic energy one is translational kinetic energy and rotational kinetic energy
Total kinetic energy = translational kinetic energy + rotational kinetic energy
$K.E = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2}$ Where $I \Rightarrow$ Moment of inertia of body
$v \Rightarrow$ Translational velocity or velocity of centre of mass
$\omega \Rightarrow$Angular velocity of body