Question

A body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
$\left( a \right)$ $\sqrt {\dfrac{{2GM}}{R}}$
$\left( b \right)$ $\sqrt {\dfrac{{GM}}{R}}$
$\left( c \right)$ $\sqrt {\dfrac{{3GM}}{R}}$
$\left( d \right)$ $\sqrt {\dfrac{{5GM}}{{4R}}}$

Answer 1

Hint Here in this question we have to find the velocity with which the body was projected and for this, we will use the conservation of energy and we know that the conservation of energy will be equal to energy at the earth's surface will be equal to the energy at the point at which the body will be after some velocity.
Formula used
Kinetic energy,
$K = \dfrac{1}{2}m{v^2}$
And potential energy,
$V = \dfrac{{ - GMm}}{R}$
Here,
$K$, will be the kinetic energy
$m$, will be the mass of the body
$v$, will be the velocity
$V$, will be the potential energy
$G$, will be the gravitational constant
$M$, will be the mass of the earth
$R$, will be the radius of the earth

Complete Step By Step Solution first of all we make the diagram to solve the question. So at the earth's surface, there is the body that is being projected from the earth’s surface. The body will cover the height which will be equal to the earth's radius.

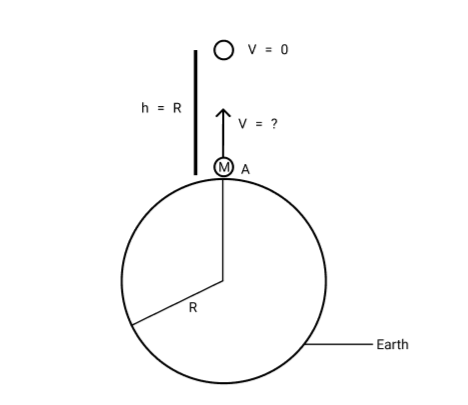
So from this, we can say that
$h = R$
Now by using the conservation of energy,
The energy at the point $A$will be equal to the energy at the point $B$
Therefore,
$K{E_A} + P{E_A} = K{E_B} + P{E_B}$
Now putting the value we know already from the formula, we get
Since at point $A$ the $PE$will be zero. And at height, $B$the kinetic energy will be zero.
Therefore,
$\Rightarrow \dfrac{1}{2}m{v^2} + \dfrac{{ - GMm}}{R} = 0 - \dfrac{{GMm}}{{R + R}}$
Now, we will solve the above equation and we get
$\Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{ - GMm}}{{2R}} + \dfrac{{GMm}}{R}$
On solving the RHS, we get
$\Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{GMm}}{{2R}}$
Since $m$is common so it will cancel out, we have left
$\Rightarrow {v^2} = \dfrac{{GM}}{R}$
Now, we will remove the root and we get
$\Rightarrow v = \sqrt {\dfrac{{GM}}{R}}$

Therefore, the option $B$ will be correct.

Note So to understand the energy conservation we should have to be clear abo it. Energy conversion means to change its form, for example when supplied current to an electric motor then electric energy is converted into mechanical energy, and pumping of water takes place. Energy conservation means to conserve energy, for example, we switch off the bulb when it is not in use, so here electrical energy is conserved.