Question
Question: A body of weight \(W=mg\) slides down a rough vertical pole with an acceleration \(\dfrac{g}{4}\) wh...
A body of weight W=mg slides down a rough vertical pole with an acceleration 4g where g is the acceleration due to gravity. What is the frictional force in terms of the weight of the body?
A)4W
B)2W
C)3W
D)43W
Solution
Hint: First of all, we will draw the diagram as per the question and then we will consider the forces acting on the body when the body slides down a rough vertical pole with an acceleration 4g. And then equation the forces with the net force acting on the body we will find the answer of the problem.
Formula used: Fnet=ma
Complete step by step answer: In the question it is given that A body of weight W=mg slides down a rough vertical pole with an acceleration 4gwhere g is the acceleration due to gravity and we are asked to find the frictional force in terms of weight of body. So, first of all, we will draw the diagram as per the question.
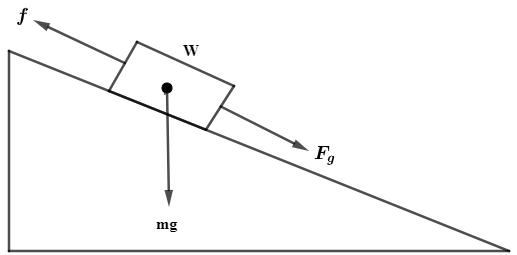
Now, in the diagram it can be observed that the object is sliding down on the rough surface due to gravity g, so we can say that gravitational force acts in the downwards on the body as shown in figure and it can be given mathematically as,
Fg=mg…………………….(i)
Now, as the body moves in downward direction, the frictional force will act in the upward direction, as the frictional force always acts in the direction opposite to the direction of motion, so the friction force can be given mathematically as,
f …………………………..(ii)
So, the net force acting on the body can be given as,
Fnet=Fg−f …………..(iii)
Now, we know that by newton's second law of motion it is said that net force acting on the body is equal to the product of mass of body and its acceleration, this can be seen mathematically as,
Fnet=ma
In question it is given that the acceleration of the body is 4g, so replacing the value of a we will get,
Fnet=4mg …………(iv)
Equating equation (iii) and (iv) we will get,
Fg−f=4mg
Now, replacing the value of gravitational force with the value from equation (i) we will get,
mg−f=4mg
Simplifying the equation further we will get,
mg−4mg=f
⇒f=mg−4mg=44mg−mg
⇒f=43mg
Now, we know that mg can also written as weight of the body W, so replacing the value we will get,
f=43W
Hence, frictional force acting on the body in terms of weight is f=43W.
Thus, option (D) is correct.
Note: In such types of problems students might make mistakes in considering the upward and downward directions of forces acting on the body and due to that they might make in calculating the sum so the answer may go wrong. So, students should take care while solving such problems.
