Question

A body of weight $W$ is suspended by a string. It is pulled aside with horizontal force of $2W$ and held at rest. The tension in it is

Answer 1

Use the formula for Newton’s second law of motion. Draw the free-body diagram of the body suspended by the string when pulled by horizontal force. Apply Newton’s second law of motion to the body in horizontal and vertical direction to determine the tension in the string.

Formula Used:
Newton’s second law of motion is given by
${F_{net}} = ma$
Here, ${F_{net}}$ is the net force on the object, $m$ is the mass of the object and $a$ is the acceleration of the object.

Complete step by step answer:
The body of weight $W$ is suspended by a string and it is pulled aside by a horizontal force of $2W$ where it is held at rest.
The free body diagram of the body is as follows;

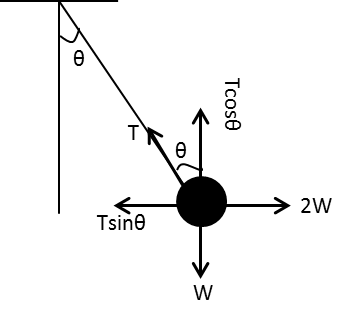
The body is pulled aside from the original position. Hence, the string makes an angle $\theta$ with the vertical.
In the above free-body diagram, $T$ is the tension in the string, $W$ is the weight of the body, $2W$ is the horizontal force on the body and $T\sin \theta$ and $T\cos \theta$ are the horizontal and vertical components of tension respectively.
Since the body is held at rest, the body is in equilibrium and the forces on the body in horizontal and vertical direction are balanced.
Apply Newton’s second law of motion to the body in the horizontal direction.
$T\sin \theta = 2W$ …… (2)
Apply Newton’s second law of motion to the body in the vertical direction.
$T\cos \theta = W$ …… (3)
Divide equation (2) by equation (3).
$\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{2W}}{W}$
$\Rightarrow \tan \theta = \dfrac{2}{1}$
The equation for the tan any angle is the ratio of the opposite side to the adjacent side of a right angle triangle.
From the above equation, it can be concluded that the opposite side is 2 and adjacent side is 1.

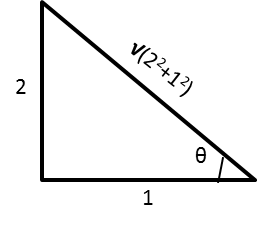
The sine of an angle is the ratio of the opposite side and hypotenuse of an angle.
From the above diagram, the sine of an angle $\theta$ is
$\sin \theta = \dfrac{2}{{\sqrt {{2^2} + {1^2}} }}$
$\Rightarrow \sin \theta = \dfrac{2}{{\sqrt 5 }}$
Substitute $\dfrac{2}{{\sqrt 5 }}$ for $\sin \theta$ in equation (2).
$\Rightarrow T\dfrac{2}{{\sqrt 5 }} = 2W$
$\Rightarrow T = \sqrt 5 W$

Hence, the tension in the string is $\sqrt 5 W$.

Note: The net vertical and horizontal forces on the body are balanced, hence, the net acceleration and the net force on the body is considered zero while applying Newton’s law.