Question

A body of weight $W$ is lying at rest on a rough horizontal surface. If the angle of friction is $\theta$ then the minimum force required to move the body along surface will be
A. $W\cos \theta$
B. $W\tan \theta$
C. $W\sin \theta$
D. $W\cot \theta$

Answer 1

In order to answer the question, to know the minimum force required to move the body along the horizontal rough surface P to be minimum, $cos{\text{ }}\left( {\theta - \phi } \right)$ should be maximum, i.e.
In other words, the effort is minimum when its inclination $\left( \theta \right)$ with the horizontal is equal to the angle of friction $\left( \phi \right)$ .

Complete step by step solution:
Firstly we will draw a diagram, after that we will proceed to the question;

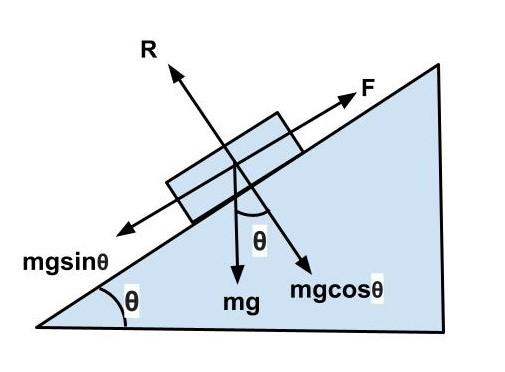
Now, coming to the question;
In the question, it is stated that;
The body is of weight $W$ is lying rest on the rough horizontal plane.
Angle of friction is given as $\theta$
Now, we know that $F = mg$ is the gravity force equation, where $g$ is the acceleration owing to gravity.
The weight of an object is also indicated using the equation $\left( {W = mg} \right)$ .
Now, we know the relationship between angle of friction and angle of repose as;
Angle of friction = Angle of repose
Because a body will be ready to move if it is placed on an inclined plane with an angle equal to the angle of repose.
Therefore,
$F = mg \times \sin \theta$
Now we will put $W$ in place of $mg$
$\therefore F = W\sin \theta$
As a result, $W\sin \theta$ is the correct solution.
The correct option is: (C) $W\sin \theta$

Note: It's also important to keep in mind that force and acceleration are not similar. When a big body encounters a net force that is not zero, it accelerates. That is, Newton's first law of motion.
The value of the acceleration is determined by Newton's second law of motion.
To put it another way, sum $F = ma$ . $F$ and $a$ are vectors, which are directed quantities.
To get an object to move upward from a standstill, you must exert an infinitesimally more upward force than the weight of the object, which is directed downward.