Question
Question: A body of weight \[200N\] is suspended with the help of string as shown in the figure. Find the tens...
A body of weight 200N is suspended with the help of string as shown in the figure. Find the tensions in the strings.
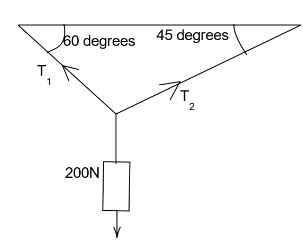
Solution
We are asked to find the tension in the strings. We can start by resolving the tension in the strings into their respective sine and cosine components. Then we can find the values that are equal and equate them with one another. This gives us the relationship between the tensions of the two strings. We have two components of each tension and this gives us two equations and two unknown values. We can solve this and get the values of tension of the two strings.
Complete step by step answer:
We can resolve the value of the tension in each string as
The x-component of the tension in the first string is, Tx=T1cos30
The y-component of the tension in the first string is, Ty=T1sin30
The x-component of the tension in the second string is, Tx=T2cos45
The y-component of the tension in the second string is, Ty=T2sin45
Free body diagram for the body is as follows:
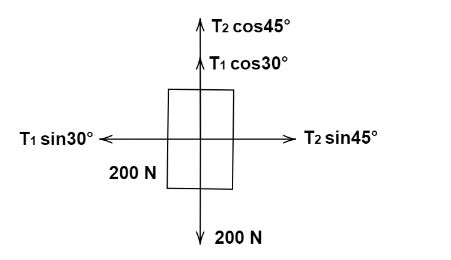
At equilibrium, the x-components of the two tensions will be equal
T1cos30=T2cos45
Substituting the values, we get a relationship between the tension values we get,
21T1=21T2
We can cross multiply and get, 2T1=2T2
Now we can move onto finding a relationship between the sine components of the two vectors.
T1sin60+T2sin45=200
As the cosine components are responsible for the mass of the block. Now, we can substitute the value of one of the tension with respect to the other and get
2T2×23+T221=200
We can solve this and get the value of T2 as,
T2=(3+1)2002
We can substitute this value in the relationship we got and get the value of the tension of the first string as,
T1=(3+1)400
Therefore, the tension in the strings are (3+1)400 and (3+1)2002.
Note: Vectors can be split into two components, the sine and cosine components.
For instance, tension is split into two components, the x-component will be Tx=TcosX. The y-component will be Ty=TsinX.
