Question

A body of mass $m$ thrown horizontally with velocity $v$ , from the top of the tower of height $h$ touches the level ground at a distance of $250m$ from the foot of the tower. A body of mass $2m$ thrown horizontally with velocity $\dfrac{v}{2}$ ​, from the top of the tower of height $4h$ will touch the level ground at a distance $x$ from the foot of the tower. The value of $x$ is:
A. $250m$
B. $500m$
C. $125m$
D. $250\sqrt 2 m$

Answer 1

To solve this question we need to use the equation of motion. The heights of the first and the second towers are given for the two cases. We need to create the first expression known displacement using the displacement formula and also we need to find another expression for unknown displacement and substitute from the first expression and we arrive at the desired solution for the question.

Complete step by step solution:

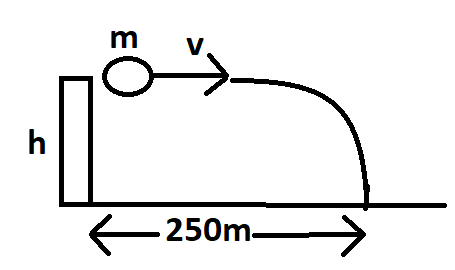
Given that the mass of the body is $m$ and the height of the tower is $h$. The body touches the ground at a distance of $250m$ from the foot of the tower. And also given that the velocity of the body is $v$.
For a free-falling object dropped from a known height, to calculate the time taken for the body to fall distance h we can use the second equation of motion.
$s = ut + \dfrac{1}{2}a{t^2}$
Here, s is the displacement of the body. In our case $s = h$. The body falls starting at rest ($u = 0$) and reaches the final velocity v. The acceleration in these types of problems will be the acceleration due to gravity. Therefore, $a = g$.
Substituting all these the equation of the motion becomes,
$h = \dfrac{1}{2}g{t^2}$
Rearranging the above equation to find time $t$ ,
$t = \sqrt {\dfrac{{2h}}{g}}$
We know the distance from the foot of the tower to the place where the object fell on the ground
$d = 250m$
$d = vt$
Therefore,
$250 = v \times \sqrt {\dfrac{{2h}}{g}}$ ….. (1)
The next case can be diagrammatically as below,

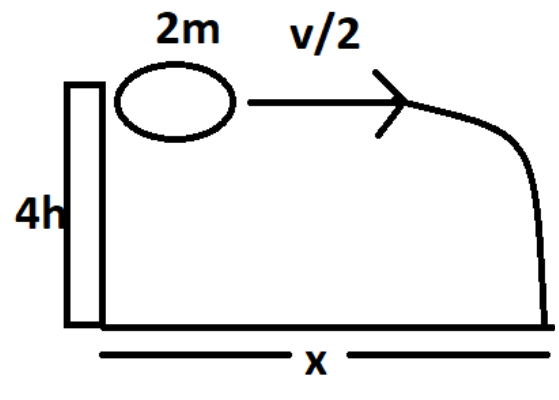
We have seen that the expression for the first case is independent of mass, similarly the second will also be independent of mass.
The height of the tower, in this case, is given as $4h$. The body touches the ground at a distance of x from the foot of the tower. We need to find this x. Given the velocity of the body is $\dfrac{v}{2}$. We already have the equation of time. Therefore we can substitute these values in the below-given formula again,
$d = vt$
$x = \dfrac{v}{2} \times \sqrt {\dfrac{{2(4h)}}{g}}$
Simplifying the above equation we get,
$x = v \times \sqrt {\dfrac{{2h}}{g}}$ …… (2)
Substituting equation (1) in (2) we get,
$x= 250 m$
Therefore, $x = 250m$m.
The correct option is A.

Note:
The motion that we have seen in the above case is a projectile motion. Projectile motion is a form of motion that refers to a body that is thrown into air or space and then travels under the influence of gravity alone. The total distance that is covered by the body during this motion is said to be the range of the projectile motion.