Question
Question: A body of mass M starts sliding down on the inclined plane where the critical angle is \[ACB={{30}^{...
A body of mass M starts sliding down on the inclined plane where the critical angle is ACB=300 as shown in the figure. The coefficient of kinetic friction will be?
(A)3Mg
(B)3Mg
(C)3
(D) None of the above
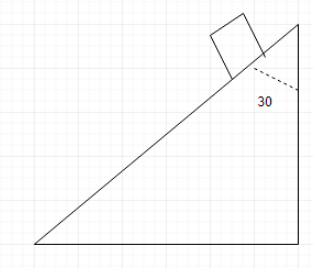
Solution
The body is sliding down. We know that frictional force always opposes the motion. So, if the body is moving downwards, the frictional force must act in the opposite direction. Here, no external force is acting on the system. We can find the value of coefficient of friction in terms of other parameters.
Complete step by step answer:
Let us draw all the forces acting on the block.We know the sum of all angles of a triangle is equal to 1800. The triangle is a right angled and one angle is 300 and one is 900, so, by using angle sum property the third angle comes out to be 600.

Normal Reaction is R=Mgcos30
The critical angle is 300, it means the block is just about to move and, in that case, Mgsin60=μMgcos60,So,
⇒Mgsin60=μMgcos60
⇒sin60=μcos60
⇒μ=tan60
∴μ=3
So, the correct option is (C).
Note: Here we were not given the angle of the inclined, so we first had used the angle sum property of the triangle to find out the angle of the inclined plane. Also, when the body is at rest, all the forces acting cancels out each other. Also, when the block is just about to move the value of the frictional force is the maximum and at that time the forces acting in the two opposite directions are just equal and we had exploited the same condition here.
