Question

A body of mass $m$ moving with a constant velocity $v$ hits another body of the mass $m$ moving with same velocity $v$ but in the opposite direction, and sticks to it. The velocity of the compound body after collision is :
(A) Zero
(B) $v$
(C) $2v$
(D) $v/2$

Answer 1

Use the law of the conservation of the momentum to calculate the final velocity. Substitute the given parameters in the formula of the momentum and cancel the similar terms to know the value of the final velocity of the balls after collision.

Useful formula:
The momentum is given by
$p = mv$
Where $p$ is the momentum, $m$ is the mass of the body and $v$ is the velocity of the body.

Complete step by step solution:
The law of conservation of momentum states that if two or more bodies collide with each other by themselves without the application of any external force, their total momentum before collision must be equal to the total momentum after the collision. Hence
Initial momentum=final momentum

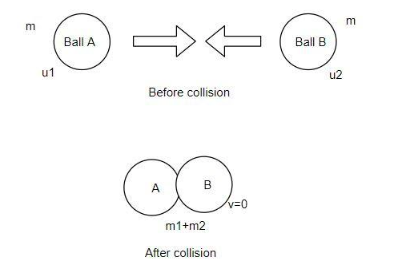
By applying the formula in the above equation,
${m_1}{u_1} - {m_2}{u_2} = {m_1}{v_1} - {m_2}{v_2}$
Here the masses of both the body and the final velocity is the same.
$m{u_1} - m{u_2} = m{v_{}} - {m_{}}{v_{}}$
By simplifying the above equation,
$m\left( {{u_1} - {u_2}} \right) = 2mv$
By cancelling the similar terms in both the sides.
${u_1} - {u_2} = 2v$
Since the velocity of the two balls are same,
${u_1} - {u_2} = 0$
The two body sticks to it forming the compound body so its final velocity is
$v = 0$
Hence the velocity of the compound body is zero.

Thus the option (A) is correct.

Note: After the collision of the two balls, if they stick to each other without moving away from them, both the balls join together. This causes the mass after the collision is the sum of the masses of the balls and the velocity gets to zero after the collision.