Question

A body of mass m is taken from the Earth’s surface to the height equal to twice the radius of the Earth. The change in potential energy of the body will be –

& \text{A) 3mgR} \\\ & \text{B) }\dfrac{1}{3}\text{mgR} \\\ & \text{C) 2mgR} \\\ & \text{D) }\dfrac{2}{3}\text{mgR} \\\ \end{aligned}$$

Answer 1

We have to use our knowledge on the variation potential energy with the height. For ease, we can initially consider the surface of the earth with zero potential energy or the height is nil. Then we can compare it with the energy at the height.

Complete answer:
We know that there will be a significant change in the potential energy of a body when the height increases. The potential energy is directly proportional to the height as –
$PE=mgh$
Where, m is the mass of the body,
g is the acceleration due to gravity near to surface of earth,
h is the height from the surface of the earth.

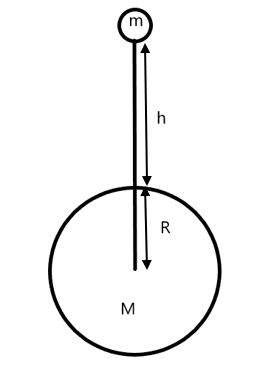
Among the above variables, we know that the acceleration due to gravity is only a constant when the body is close to the surface. So, in this situation, we have to consider the change in this constant due to the height.
From the Newton’s gravitational law,
$F=\dfrac{GMm}{{{R}^{2}}}$
Where, F is the force between two masses M (mass of earth) and m (the body),
G is the gravitational constant,
R is the radius of the earth.
We derived the acceleration due to gravity from this constant as –
$g=\dfrac{GM}{{{R}^{2}}}$
Now, we know that the distance between the center of the earth and the body is not R, so we have to find the new acceleration due to gravity as –

& {{g}^{,}}=\dfrac{GM}{{{(R+h)}^{2}}} \\\ & \Rightarrow \text{ }{{g}^{,}}=\dfrac{GM}{{{R}^{2}}+{{h}^{2}}+2Rh} \\\ & \text{the above equation can be simplified as - } \\\ & {{\text{g}}^{,}}=g(\dfrac{1}{1+h/R}) \\\ \end{aligned}$$ Let us apply this to our situation, We are given that, $$\begin{aligned} & h=2R, \\\ & \Rightarrow \text{ }PE=m{{g}^{,}}h \\\ & \Rightarrow \text{ }PE=\dfrac{mgh}{1+h/R}=\dfrac{mghR}{R+h} \\\ & \Rightarrow \text{ }PE=\dfrac{mg(2R)R}{R+2R} \\\ & \Rightarrow \text{ }PE=\dfrac{2}{3}mgR \\\ \end{aligned}$$ So, we have found the potential energy of the body of mass ‘m’ at a height twice as the radius of the earth to be $$\dfrac{2}{3}mgR$$. **So, the correct answer is “Option D”.** **Note:** When finding the acceleration due to gravity at a height h above the surface, we can neglect the higher orders of the ‘h’ in the denominator as we have done here. The acceleration due to gravity reduces as we go up or down the surface of the earth.