Question

A body of mass ‘m’ is taken from the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be-
A) mg2R
B) $\dfrac{2}{3}$ mgR
C) 3 mgR
D) $\dfrac{1}{3}$ mgR

Answer 1

We will be drawing a diagram to trace the change in position of the object.
The formula for potential energy will be applied when the object is on the surface of the earth and on height respectively.
$U = - \dfrac{{G{m_1}{m_2}}}{{{R^{}}}}$ where,
G = Gravitational constant
${m_1}$ and ${m_2}$ = Mass of the objects
R = Distance from the centre.
As the options are given in g, the following relationship can be used:
$g = \dfrac{{GM}}{{{R^2}}}$

Complete step by step answer: Mass of body = m (given)
Let mass of the earth = M
Radius of the earth = R (given)
Representing the change in position of the body with diagram:

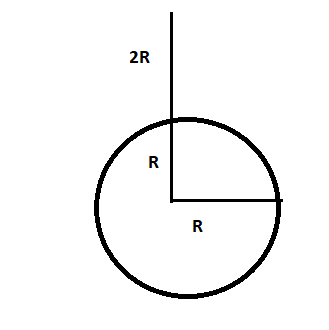
The potential energy (U) is given as:
$U = - \dfrac{{GMm}}{{{R^{}}}}$
Potential energy on the surface (s) of the earth and at height (h) twice the radius (2R) :
${U_s} = - \dfrac{{GMm}}{{{R^{}}}}$ _____________ (1)
${U_h} = - \dfrac{{GMm}}{{R + 2{R^{}}}} \\\ \\\$
As the distance is measured from the center of the earth.
${U_h} = - \dfrac{{GMm}}{{3{R^{}}}}$ ____________ (2)

The change in potential energy $\left( {\Delta U} \right)$ is given by the difference between (1) and (2)
$\Delta U = {U_h} - {U_s}$
Substituting the values from (1) and (2):
$\Delta {U_{}} = - \dfrac{{GMm}}{{3{R^{}}}} - \left( { - \dfrac{{GMm}}{{{R^{}}}}} \right)$
$\Delta {U_{}} = \dfrac{2}{3}\dfrac{{GMm}}{{{R^{}}}}$ ____________ (3)
But the options are given in g which is acceleration due to gravity whose relationship with G (Gravitational constant) can be given as:
$g = \dfrac{{GM}}{{{R^2}}}$
$G = \dfrac{{g{R^2}}}{M}$
Substituting this value of G in (3):
$\Delta {U_{}} = \dfrac{2}{3}\dfrac{{\dfrac{{g{R^2}}}{M}Mm}}{{{R^{}}}}$

$\Delta {U_{}} = \dfrac{2}{3}mgR$
Therefore, the change in potential energy when a body of mass ‘m’ is taken from the earth's surface to the height equal to twice the radius of the earth will be $\dfrac{2}{3}mgR$, option B)

Note: Negative potential energy represents the force of attraction. Gravitational force is an attractive force and hence the potential energy of the body is taken as negative.
Acceleration due to gravity (g) and gravitational constant (G) both have values 9.8 m/s and$6.67 \times {10^{ - 11}}{m^3}k{g^{ - 1}}{s^{ - 2}}$ respectively.