Question
Question: A body of mass m is suspended by two strings making angles\[\alpha \] and\[\beta \] with the horizon...
A body of mass m is suspended by two strings making anglesα andβ with the horizontal. Tensions in two strings are
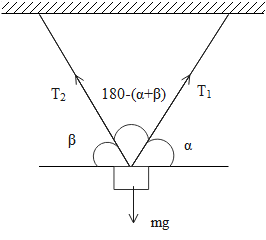
Solution
The horizontal components of the tensions balance each other when the body will be in equilibrium. Similarly, the vertical components of the tension balance the weight of the body. So, using these conditions, we will find the expressions for the same and will compute the expressions for the tensions.
Complete answer:
Firstly we will consider a diagram representing the directions of the horizontal and vertical components of the tension working on the string.
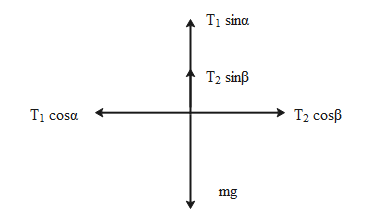
The horizontal components of T1and T2balance each other as the body is in equilibrium.
T1cosα=T2cosβ
T2=cosβT1cosα…… (1)
The vertical components of T1and T2balance the weight of the body.
T1sinα+T2sinβ=mg…. (2)
Substitute the equation (1) in equation (2).
