Solveeit Logo
Login

Question

Question: A body of mass M collides against a wall with velocity V and retraces its path with the same speed. ...

A body of mass M collides against a wall with velocity V and retraces its path with the same speed. The change in momentum is
(take initial direction of velocity as positive)
A. zero
B. 2MV2MV
C. MVMV
D. −2MV - 2MV

Explanation

Solution

Momentum of a body is defined as the product of the mass of the body and the velocity with which the body is travelling. Change in momentum is the difference between final momentum and initial momentum. Calculate the initial momentum by taking velocity as positive because the body moves against the wall and final momentum by taking the velocity as negative because the body moves away from the wall as the direction is changed.

Complete step by step answer:
We are given that a body of mass M collides against a wall with velocity V and retraces its path with the same speed.

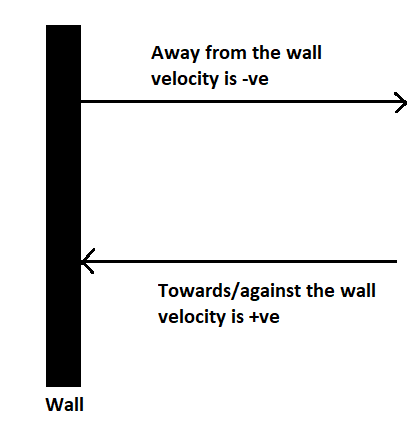
We have to calculate the change in momentum of the body.
Change in momentum is the difference of initial and final momentums, whereas momentum is the product of mass and velocity.
ΔP=Pf−Pi\Delta P = {P_f} - {P_i}
Initially, the body travels with a velocity V, which is positive.
Initial momentum is Pi=M×V=MV{P_i} = M \times V = MV
The body retraces which means it moves away from the wall with the same velocity but in the opposite direction, so the final velocity will be –V, which is negative.
Final momentum is Pf=M×−V=−MV{P_f} = M \times - V = - MV
Change in momentum of the body will be
ΔP=Pf−Pi Pf=−MV Pi=MV ΔP=−MV−(MV) ∴ΔP=−MV−MV=−2MV  \Delta P = {P_f} - {P_i} \\\ {P_f} = - MV \\\ {P_i} = MV \\\ \Delta P = - MV - \left( {MV} \right) \\\ \therefore \Delta P = - MV - MV = - 2MV \\\

So, the correct answer is “Option D”.

Note:
Another approach to solve the above question
Change in momentum is the product of mass and change in velocity.
ΔP=M×ΔV ΔV=Vf−Vi  \Delta P = M \times \Delta V \\\ \Delta V = {V_f} - {V_i} \\\
Mass of the body is the same, but the velocity is changed.
Initial velocity is V and final velocity is –V, as the direction of the velocity is changed when moving away from the wall.
Vi=V,Vf=−V ΔV=−V−(V)=−V−V=−2V ΔP=M×ΔV   ⟹  ΔP=M×(−2V) ∴ΔP=−2MV  {V_i} = V,{V_f} = - V \\\ \Delta V = - V - \left( V \right) = - V - V = - 2V \\\ \Delta P = M \times \Delta V \\\ \implies \Delta P = M \times \left( { - 2V} \right) \\\ \therefore \Delta P = - 2MV \\\
The change in momentum of the body is −2MV - 2MV