Question

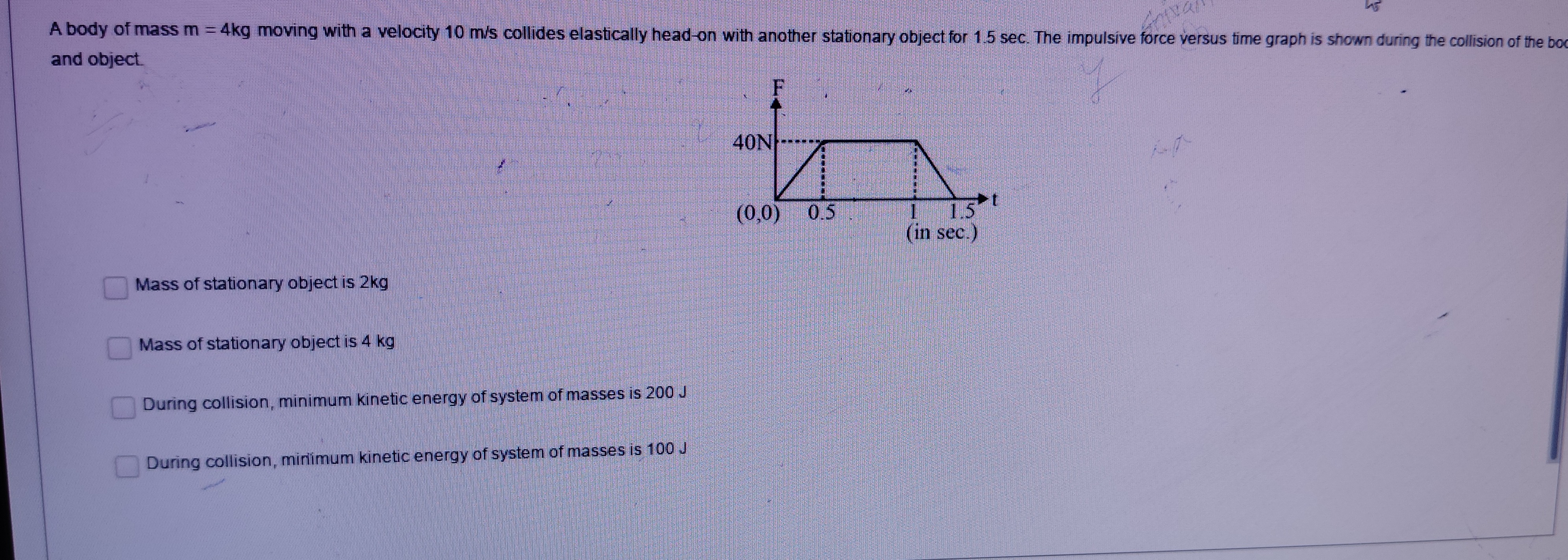
A body of mass m = 4kg moving with a velocity 10 m/s collides elastically head-on with another stationary object for 1.5 sec. The impulsive force versus time graph is shown during the collision of the boo and object.

• A. Mass of stationary object is 2kg
• B. Mass of stationary object is 4 kg
• C. During collision, minimum kinetic energy of system of masses is 200 J
• D. During collision, minimum kinetic energy of system of masses is 100 J

Answer 1

Answer: (B), (D)

Mass of stationary object is 4 kg, During collision, minimum kinetic energy of system of masses is 100 J

Answer 2

The given problem describes a head-on elastic collision between a body of mass $m_1 = 4$ kg moving with a velocity $v_{1i} = 10$ m/s and a stationary object of mass $m_2$ with initial velocity $v_{2i} = 0$ m/s. The collision lasts for 1.5 seconds, and the impulsive force versus time graph is provided.

First, let's calculate the total impulse delivered during the collision. The impulse is the area under the force-time graph. The graph is composed of a triangle from $t=0$ to $t=0.5$ s, a rectangle from $t=0.5$ s to $t=1$ s, and a triangle from $t=1$ s to $t=1.5$ s.

Area of the first triangle = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 0.5 \times 40 = 10$ Ns. Area of the rectangle = $\text{base} \times \text{height} = (1 - 0.5) \times 40 = 0.5 \times 40 = 20$ Ns. Area of the second triangle = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times (1.5 - 1) \times 40 = \frac{1}{2} \times 0.5 \times 40 = 10$ Ns. Total impulse $J = 10 + 20 + 10 = 40$ Ns.

The impulse is equal to the change in momentum. Let's assume the initial velocity of the moving body is in the positive direction. The force exerted by the stationary object on the moving body is in the opposite direction, so the impulse on the moving body is negative. The impulse on the stationary object is positive.

Impulse on body 1 = $m_1 (v_{1f} - v_{1i}) = -J$. $4 (v_{1f} - 10) = -40$. $v_{1f} - 10 = -10$. $v_{1f} = 0$ m/s.

Impulse on body 2 = $m_2 (v_{2f} - v_{2i}) = J$. $m_2 (v_{2f} - 0) = 40$. $m_2 v_{2f} = 40$.

Since the collision is elastic and head-on, we have the relation for relative velocities: $v_{2f} - v_{1f} = -(v_{2i} - v_{1i})$. $v_{2f} - 0 = -(0 - 10)$. $v_{2f} = 10$ m/s.

Now substitute $v_{2f} = 10$ m/s into the impulse equation for body 2: $m_2 \times 10 = 40$. $m_2 = \frac{40}{10} = 4$ kg. So, the mass of the stationary object is 4 kg. This matches the second option.

Now let's consider the minimum kinetic energy of the system during the collision. The minimum kinetic energy occurs at the moment of maximum compression, where the two bodies have the same velocity. Let this common velocity be $v$.

By conservation of momentum up to the moment of maximum compression: $m_1 v_{1i} + m_2 v_{2i} = m_1 v + m_2 v$. $4 \times 10 + 4 \times 0 = (4 + 4) v$. $40 = 8v$. $v = \frac{40}{8} = 5$ m/s.

At the moment of maximum compression, the kinetic energy of the system is: $K_{min} = \frac{1}{2} m_1 v^2 + \frac{1}{2} m_2 v^2 = \frac{1}{2} (m_1 + m_2) v^2$. $K_{min} = \frac{1}{2} (4 + 4) \times 5^2 = \frac{1}{2} \times 8 \times 25 = 4 \times 25 = 100$ J. So, the minimum kinetic energy of the system of masses is 100 J. This matches the fourth option.

Let's check the options:

• Mass of stationary object is 2kg (Incorrect)
• Mass of stationary object is 4 kg (Correct)
• During collision, minimum kinetic energy of system of masses is 200 J (Incorrect, this is the initial and final kinetic energy)
• During collision, minimum kinetic energy of system of masses is 100 J (Correct)

The question asks for the correct options, so there can be multiple correct options. Based on our calculations, the mass of the stationary object is 4 kg and the minimum kinetic energy of the system is 100 J.