Question

A body of mass 6 kg rests in limiting equilibrium on an inclined plane whose slope is ${{30}^{\circ }}$ . If the plane is raised to slope of ${{60}^{\circ }}$ , then the force (in kg-wt) along the plane required to support it is

& ~A.~~~~~~~~~3 \\\ & ~B.~~~~~~~~2\sqrt{3} \\\ & ~C.~~~~~~~~~\sqrt{3} \\\ & ~D.~~~~~~~~~3\sqrt{3} \\\ \end{aligned}$$

Answer 1

Hint: As the slope is inclined a component of its weight will be pulling it downwards, as the body is at rest friction force will be acting on it. We can find this force and use it so find how much extra force is needed to hold the body at rest when inclination is increased.

Formula Used: Newton’s second law of motion F = ma, m is mass & a is acceleration maximum frictional force possible =$\mu N$, N is normal against the surface & $\mu$ is coefficient of friction.

Complete step-by-step answer:
__
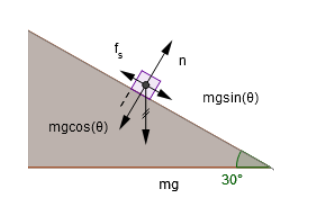
Here, m is mass of body, g is acceleration due to gravity, f is maximum sliding friction, n is normal from incline, $\theta$ is angle of incline and mg is broken into components along and perpendicular to the surface.
When the angle of incline is ${{30}^{\circ }}$ , as there is no acceleration perpendicular to surface, net force perpendicular to surface must be zero (Newton’s second law of motion). So,
$n=mg\cos \theta$
$n=6g\cos {{30}^{\circ }}$
$n=3\sqrt{3}g$

Now since the body is in limiting equilibrium i.e. just about to slide then friction will have its maximum possible value. So,
$f=\mu n$
$f=3\sqrt{3}g\mu$ ... (1)
Also the body is at rest along the incline. Hence net force along the incline is zero. So,
$f=mg\sin \theta$
Putting value of f from equation (1) and putting given value
$3\sqrt{3}g\mu =6g\sin {{30}^{\circ }}$
$3\sqrt{3}\mu =6g\times \dfrac{1}{2}$
$\mu =\dfrac{1}{\sqrt{3}}$

Here, m is mass of body, g is acceleration due to gravity, f is maximum sliding friction, n is normal from incline, $\theta$ is angle of incline which is now ${{60}^{\circ }}$and mg is broken into components along and perpendicular to the surface.
When the angle of incline is ${{30}^{\circ }}$ , as there is no acceleration perpendicular to surface, net force perpendicular to surface must be zero (Newton’s second law of motion). So,
$n=mg\cos \theta$
$n=6g\cos {{60}^{\circ }}$
$n=3g$
The maximum possible friction force is
$f=\mu \times n$
$f=\dfrac{3g}{\sqrt{3}}=\sqrt{3}g$
Component of force due to gravity along the incline is
$mg\sin \theta =6g\sin {{60}^{\circ }}=3\sqrt{3}g$
So net force along the incline is down the incline with magnitude,
$\begin{aligned} & 3\sqrt{3}g-\sqrt{3}g=2\sqrt{3}g \\\ & \\\ \end{aligned}$
Hence an extra force of $2\sqrt{3}g$ N or $2\sqrt{3}$ kg-wt is required upward along the incline.
So the correct option is B.

Note: Our final answer was $2\sqrt{3}g$N. But options are given in kg-wt, so we have to convert N in kg-wt. 1 kg-wt is the amount of force by which earth pulls the mass of 1 kg body i.e. weight of 1kg body. Therefore, 1kg-wt = g N or 1 N =1/g kg-wt. Hence,
$2\sqrt{3}g$ N = $2\sqrt{3}$ kg-wt.
Also the mentioned term “limiting equilibrium“ tells that the body is in equilibrium but just about to move.