Question

A body of mass $5kg$ moving with a speed of $1.5m/s$ on a horizontal smooth surface collides with a nearly weightless spring of force constant $k=5N/m$ . The maximum compression of the spring would be

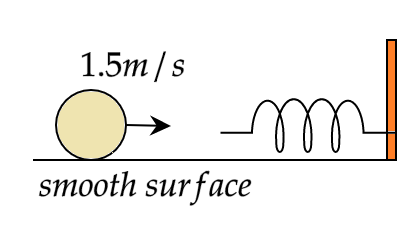
(A) $0.5m$
(B) $0.15m$
(C) $1.5m$
(D) $0.12m$

Answer 1

Hint
In the given question, we have been given the velocity of the body before the collision with the spring and we have been asked the maximum compression of the spring. Now we know that every moving body has kinetic energy and every object at rest some stored potential energy. We will use the concept of energy conservation and transformation to relate the energy of the spring with the energy of the ball. Let’s dive into the detailed solution.
Formula Used: $PE=\dfrac{1}{2}k{{x}^{2}}$ , $KE=\dfrac{1}{2}m{{v}^{2}}$

Complete step by step answer
Step by Step Solution:
When the moving ball in the given question collides with the spring, it transfers its energy to the spring. Now the spring will take that energy and start the motion but it’ll keep converting energy into potential energy as it is compressed. At the point of maximum compression, the entire energy that was transferred to the spring by the ball has been converted into potential energy of the spring.
We have been given that,
Mass of the body $(m)=5kg$
The velocity of the body $(v)=1.5m/s$
We know that kinetic energy of a body is expressed as $KE=\dfrac{1}{2}m{{v}^{2}}$
Substituting the values, we get the value of kinetic energy of the moving ball as
$\Rightarrow KE=\dfrac{1}{2}\times 5\times {{(1.5)}^{2}}$
$\Rightarrow KE=\dfrac{1}{2}\times 5\times 2.25$
$\Rightarrow KE=5.625J$
We know that the expression for the potential energy of a spring is $PE=\dfrac{1}{2}k{{x}^{2}}$ where $k$ is the spring constant and $x$ is the compression of the spring
Now, at the state of maximum compression of the spring, the potential energy of the spring can be given as $PE=\dfrac{1}{2}\times 5\times {{l}^{2}}$ where $l$ is the maximum compression of the spring
Relating the kinetic energy of the moving ball with the potential energy of the spring (because no energy loss anywhere in the system), we can say that
$\Rightarrow \dfrac{1}{2}\times 5\times {{l}^{2}}=5.625J$
$\Rightarrow 2.5\times {{l}^{2}}=5.625J$
$\Rightarrow {{l}^{2}}=2.25{{m}^{2}}$
$\Rightarrow l=1.5m$
Hence we can say that the maximum compression of the spring is $1.5m$ or option (C) is the correct answer.

Note
Here the surface on which the ball rolls is given is smooth, hence we can say that no friction force will be acting on the moving ball. In the absence of friction, the body’s speed or velocity will remain unchanged with time and we can say that only conservative forces are acting on our system. Thus the energy of the system of the ball and the spring remains constant and we can interchange the values of kinetic and potential energies to find the answer.
If friction was acting, we would have to calculate the loss in energy due to friction and then proceed with our solution.