Question

A body of mass 5kg is at rest. Three forces ${{F}_{1}}=10N$ due north, ${{F}_{2}}=10N$ along east and ${{F}_{3}}=10\sqrt{2}N$ along N-W act on it simultaneously. The acceleration produced in the body is
A. $4m{{s}^{-2}}$ along North
B. $2m{{s}^{-2}}$ along North
C. $4m{{s}^{-2}}$ along East
D. $2m{{s}^{-2}}$ along East

Answer 1

Use the formula for the magnitude of the resultant vector of two vectors. First find the resultant force between the first two forces and then find the net force acting on the body. later calculate the acceleration of the body.

Formula used:
$R=\sqrt{{{A}^{2}}+{{A}^{2}}+2AB\cos \theta }$,
where R is the resultant of the vectors A, B and $\theta$ is the angle between A and B.
$a=\dfrac{F}{m}$,
where a is the acceleration of the body of mass m when a net force F is applied on it.

Complete step by step answer:
First draw the vector diagram of the given force on the Cartesian plane by taking the positive x-axis along the east and the positive y-axis along the north.

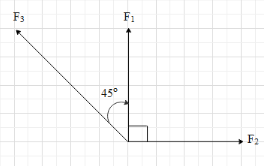
We can see that the angle between the forces ${{F}_{1}}$ and ${{F}_{2}}$ is 90 degrees and their magnitudes are 10N each, Therefore, the direction of the resultant force of the two is equal ${{F}_{12}}=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos ({{90}^{\circ }})}$
${{F}_{12}}=\sqrt{{{10}^{2}}+{{10}^{2}}+2(10)(10)(0)}=10\sqrt{2}N$.
This means the magnitude of the resultant of the first two forces is $10\sqrt{2}N$.

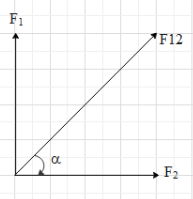
From the figure we can write that,
$\tan \alpha =\dfrac{{{F}_{1}}}{{{F}_{2}}}\\\ \Rightarrow\tan \alpha =\dfrac{10}{10}\\\ \Rightarrow\tan \alpha =1$
$\Rightarrow \alpha ={{\tan }^{-1}}1={{45}^{\circ }}$
This means that the angle between the positive x-axis and the force ${{F}_{12}}$ is ${{45}^{\circ }}$.Therefore, the resultant of the first two forces is along the direction North-east and its magnitude is $10\sqrt{2}N$.

It is given that the magnitude of the third force is ${{F}_{3}}=10\sqrt{2}N$ and it is along the North-west. This means that this force makes an angle of ${{45}^{\circ }}$ with the positive y-axis. This implies that the angle between the forces ${{F}_{12}}$ and ${{F}_{3}}$ is ${{45}^{\circ }}+{{45}^{\circ }}={{90}^{\circ }}$.
Therefore, the resultant of these two forces is equal to ${{F}_{123}}=\sqrt{F_{12}^{2}+F_{3}^{2}+2{{F}_{12}}{{F}_{2}}\cos ({{90}^{\circ }})}$
$\Rightarrow {{F}_{123}}=\sqrt{{{\left( 10\sqrt{2} \right)}^{2}}+{{\left( 10\sqrt{2} \right)}^{2}}+2(10\sqrt{2})(10\sqrt{2})(0)}\\\ \Rightarrow {{F}_{123}} =20N$.
And the direction of this force is along the north. Therefore, we get that the net force on the body is 20N along the north. This means that the acceleration of the body is,
$a=\dfrac{F}{m}\\\ \Rightarrow a =\dfrac{20}{5}\\\ \therefore a =4m{{s}^{-2}}$ along north.

Hence, the correct option is A.

Note: A body accelerates in the direction of the net force applied on it. The direction of the velocity of the body at a certain time may be different but the direction of its acceleration will be along the direction of the net force.The resultant force is described as the total amount of force acting on the object or body along with the direction of the body. The resultant force is zero when the object is at rest or it is traveling with the same velocity as the object. The resultant force should be equal for all the force since all the force is acting in the same direction.