Question

A body of mass 500 gm is tied to one end of a string of length 1m and is whirled round in a horizontal circle making 2 revolutions per seconds. Calculate the tension in the string.
(A) 78.88N
(B) 7.888N
(C) 0.7888N
(D) 7888N

Answer 1

Centrifugal force is the force that arises from inertia of the body undergoing circular motion. The reaction force of centrifugal force is centripetal force. The tension in the string is caused by the centripetal force acting on the string to balance the centrifugal force. Therefore the tension in the string can be calculated by simply calculating the centrifugal force.
Formula used:
F = m${{\omega }^{2}}r$

Complete answer:
When a body of a certain mass is tied to the end of a string and whirled, centrifugal force comes to play. The tension caused in the string is due to the reaction force caused by the centrifugal force as a result of Newton’s third law of motion.
Thus, the tension in the string can be calculated by calculating the magnitude of the centrifugal force of the stone undergoing circular motion due to the whirling.

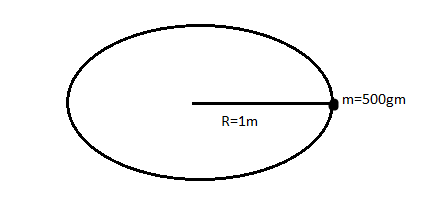
Fig: mass tied at the end of a string being whirled
Given,
m= 500 gm
=0.5 kg
The radius of the circle is given by the length of the horizontal portion of the string=1m
The frequency is given by the number of revolutions made per second=2${{s}^{-1}}$
Thus, the angular velocity of the circular motion is given as,$\omega$
$\begin{aligned} & 2\pi f \\\ & =2\pi \times 2 \\\ & =4\pi \text{ radians} \\\ \end{aligned}$
$\therefore \omega =4\pi$ Radians
Now, the formula for centrifugal force is given by, F=$m{{\omega }^{2}}r$
This centrifugal acceleration provides tension, T in the string.

$\therefore$ T= $m{{\omega }^{2}}r$
$\begin{aligned} & \Rightarrow T=0.5\times {{(4\pi )}^{2}}\times 1 \\\ & \Rightarrow T=78.88N \\\ \end{aligned}$

So, the correct answer is “Option A”.

Additional Information:
Centrifugal force is an inertial force to keep a body moving in a curved or a circular path. It is directed outwards. On the other hand, the centripetal force is directed inwards towards the centre of rotation. These forces necessarily are observed when an object is viewed from a rotating frame of reference.

Note:
In this problem, it is important to note that the tension in the string is balanced by the centrifugal force acting on the string in the outward direction. Simply grasping this concept makes the problem very easily solvable. Another point to note is that the length of the string acts as the radius in circular motion.