Question

A body of mass 40kg resting on a rough horizontal surface is subjected to a force P which is just enough to start the motion of the body. If ${{\mu }_{S}}=0.5,{{\mu }_{K}} = 0.4,\text{ }g = 10m/{{s}^{2}}$ and the force P is continuously applied on the body, then the acceleration of the body is:
$\begin{aligned} & a)zero \\\ & b)1m/{{s}^{2}} \\\ & c)2m/{{s}^{2}} \\\ & d)2.4m/{{s}^{2}} \\\ \end{aligned}$

Answer 1

In the above question we are asked to determine the acceleration of the body, such that the force P is acted upon continuously. First we will find the minimum force required to set the body in motion. Further we will determine the force to due friction when the body is in motion. When the body is in motion since it is given to us that P is acted continuously, we will obtain the net force on the body and using Newton's second law we will obtain the acceleration of the body.

Formula used:
${{F}_{NET}}=ma$
$N=mg$
${{F}_{FRIC}}=\mu N$

Complete step by step answer:
When a body is at rest on a rough horizontal surface, we have to apply some minimum amount of force until the body does not move. This depends on the coefficient of static friction (${{\mu }_{S}}$). If ‘N’ is the normal force on the body the force of static friction is given by ${{F}_{FRIC}}={{\mu }_{S}}N$.

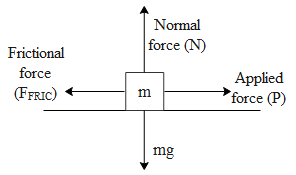
The normal force on the body is equal and opposite to the gravitational force on the body i.e. mg, hence we can say that N=mg. Therefore the minimum force(P) required to set the above body into motion,
$\begin{aligned} & P={{\mu }_{S}}N \\\ & \Rightarrow P={{\mu }_{S}}mg\text{, }\because {{\mu }_{S}}=0.5 \\\ & \Rightarrow P=0.5(40kg\times 10m{{s}^{-2}}) \\\ & \therefore P=200N \\\ \end{aligned}$
When the body is in motion the kinetic friction will try to oppose the motion of the body. If ${{\mu }_{K}}$is the coefficient of kinetic friction, the force of friction (f) on the body is equal to,
$\begin{aligned} & f={{\mu }_{K}}N\text{, }\because {{\mu }_{K}}=0.4 \\\ & \Rightarrow f=0.4\times 400N \\\ & \therefore f=160N \\\ \end{aligned}$
Let us say the acceleration of the above body is ‘a’. By Newton’s second law the Force F on the body is equal to, $F=ma$. From the above free body diagram of the we get the net force F as,
$\begin{aligned} & F=P-f \\\ & ma=200N-160N \\\ & \therefore a=\dfrac{40N}{40Kg}=1m/{{s}^{2}} \\\ \end{aligned}$

So, the correct answer is “Option B”.

Note:
The static friction comes into the picture when the body is stationary. Similarly the kinetic fiction comes into play when the body is in motion. This basically happens because friction is a self adjusting force. It is also to be noted that all the quantities mentioned have to be expressed in SI units so that the final answer is also in standard units.