Question

A body of mass $400g$ slides on a rough horizontal surface if the frictional force is $3.0N$. Find out the angle made by the contact force on the body with the vertical.
$\begin{aligned} & A.37{}^\circ \\\ & B.53{}^\circ \\\ & C.63{}^\circ \\\ & D.27{}^\circ \\\ \end{aligned}$

Answer 1

First of all draw a figure showing the details in it. The tangent of the angle between the resultant and the normal force is given as the coefficient of the friction. Substitute the values mentioned in the question. These all may help you to solve this question.

Complete step by step answer:
First of all let us draw the diagram showing the details explained in the question.

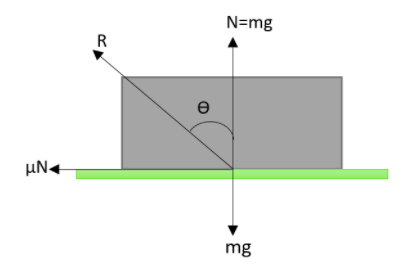
The figure shows the forces acting on the body. The contact forces in this question are the normal reaction force given as $N$ and friction force $\mu N$. The resultant of these two contact forces are found to be as $R$. Let $R$ make an angle $\theta$ with the vertical as shown in figure.
Therefore we can write that the tangent of the angle between the resultant and the normal force is given as,
$\tan \theta =\dfrac{\mu N}{mg}=\mu$
Here the normal force is given as,
$N=mg$
This means that the tangent of the needed angle is the coefficient of friction.
It has been given that the frictional force as,
$F=3N$
Now we have to find the normal force, which is given by the equation,
$N=mg$
The mass has been mentioned as,
$m=400g=0.4kg$
Substituting this in the equation will give,
$N=0.4\times 9.8=3.92$
As the frictional force can be written as,
$F=\mu N=\mu mg$
Substituting the values in it, will give,
$F=\mu N=\mu \times 3.92=3$
From this we can find the value of coefficient of friction which is given as,
$\mu =\dfrac{3}{3.92}=0.765$
Therefore the required angle will be,
$\begin{aligned} & \tan \theta =\mu \\\ & \theta ={{\tan }^{-1}}\mu =37{}^\circ \\\ \end{aligned}$
Therefore the correct answer is obtained.

Note:
Frictional force is the force which arises when two surfaces are in relative motion which are in contact. This will be the preventive force against the motion of the body. Kinetic frictional force and static frictional force are the two examples for this.