Question

A body of mass 2kg makes an elastic collision with a second body at rest and continues to move in the original direction but with one-fourth of its original speed. What is the mass of the second body?

Answer 1

- Hint: Analyse the velocities and energies of both the masses before the collision and after the collision. Then use conservation of energy and momentum theory.

Complete step-by-step solution -
Let us analyse the question. It is said that a body of mass 2kg with some initial constant velocity (u) collides with another body (mass m) at rest.

Let us assume that there is no gravity affecting both bodies and there are no external forces applied on the system of the two bodies. That means the net force on the system of the two bodies is zero. Therefore, the net momentum of the system will be constant or you can also say, the momentum of the system is conserved. In addition, it is said to be an elastic collision so there will be no loss of energy in the form of heat or sound. That means the total energy of the system is constant (conserved).
Further, it is said that after collision the 2kg body moves in the direction as initially with one-fourth of its initial velocity. Since the body whose mass is unknown was at rest and the 2kg body hit it from the right hand side direction(as shown in the above figure), it will apply a force directed towards the left on the unknown body. As a result, the unknown body will move towards the left. (If it is not clear or not true, we can just assume the velocity of the unknown body to ‘v’ towards the left. If it is true, we will get a positive value of v and if it is not true, we will get a negative value of v, which means it is moving in the opposite direction with speed ‘v’).

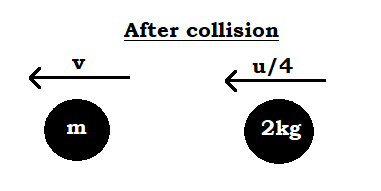
Now, to find the mass of the unknown body, we can use the law of conservation of energy and momentum.
Use the law of conservation of momentum. It says the initial net momentum is the same as the final net momentum.
Therefore, ${{\overset{\to }{\mathop{p}}\,}_{i}}={{\overset{\to }{\mathop{p}}\,}_{f}}$ Where ${{\overset{\to }{\mathop{p}}\,}_{i}}$ and ${{\overset{\to }{\mathop{p}}\,}_{f}}$ are initial and final net momentum respectively. Here, ${{\overset{\to }{\mathop{p}}\,}_{i}}=-2u$ and ${{\overset{\to }{\mathop{p}}\,}_{f}}=-mv-(2).\left( \dfrac{u}{4} \right)$.
$\Rightarrow -2u=-mv-(2).\left( \dfrac{u}{4} \right)$
$\Rightarrow 2u=mv+\left( \dfrac{u}{2} \right)$
$\Rightarrow v=\dfrac{3u}{2m}$ …….(1)
Now, use the law of conservation of energy. It says that the initial total energy is same as final total energy of the system i.e. ${K.E.}_i = {K.E.}_f$ (here it is kinetic energy).
In this case, $\text{K}\text{.}{{\text{E}}_{\text{i}}}\text{=}\dfrac{1}{2}.(2){{u}^{2}}\text{ =}{{u}^{2}}$
$K.{{E}_{f}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}.(2){{\left( \dfrac{u}{4} \right)}^{2}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{{{u}^{2}}}{16}$
Therefore,
${{u}^{2}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{{{u}^{2}}}{16}$
$\Rightarrow \dfrac{15{{u}^{2}}}{16}=\dfrac{1}{2}m{{v}^{2}}$.……(2)
Now substitute the value ‘v’ from equation (1) into equation (2)

$\Rightarrow \dfrac{15{{u}^{2}}}{16}=\dfrac{1}{2}m{{\left( \dfrac{3u}{2m} \right)}^{2}}$
$\Rightarrow \dfrac{15{{u}^{2}}}{8}=\dfrac{9{{u}^{2}}}{4m}$
$\Rightarrow m=\dfrac{6}{5}=1.2kg$
Therefore, the mass of the unknown body is 1.2kg.

Note: It is not always that the total kinetic energy of the system will be conserved. Here, since it was an elastic collision there will not be any deformation in the two bodies and they will completely restore their size after collision. In addition, it is assumed that there will not be any loss of energy in the form of heat and sound.
Practically, all collisions are inelastic. No collision is without any heat loss.