Question

A body of mass $2{\text{ }}kg$ is dropped from the rest position $5{\text{ }}m$ above the ground. What is its velocity at height $3.0{\text{ }}m$ above the ground approximately?

Answer 1

We have to use the relation between final velocity of the particle, initial velocity of the particle, acceleration of the particle, distance covered by the particle to find the final velocity. We have to consider the initial velocity as zero since it starts from the rest.

Complete step by step answer:
It is given in the question that a body of mass $2{\text{ }}kg$ is dropped from a rest position at a height of $5{\text{ }}m$ above the ground.

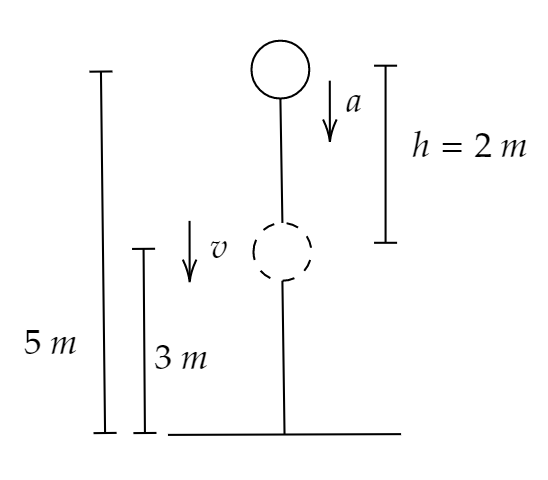
Let the initial velocity be $u$.
So, the initial velocity here is $u = 0$ as the particle is dropped from its rest position.
Let the final velocity of the body be $v$.
The height to which the velocity is to be measured is $h = 2.0{\text{ }}m$ from the initial point.
From the motions equation we get,
${v^2} - {u^2} = 2as$
The variables are defined as,
$v =$ final velocity of the particle
$u =$ initial velocity of the particle
$a =$ acceleration of the particle
$s =$ distance covered by the particle
In the given question,
$u = 0$, $a = g =$ acceleration due to gravity$= 9.8{\text{ }}\dfrac{m}{{{s^2}}}$ and $s = h =$ height covered by the particle $= \left( {5 - 3} \right) = 2{\text{ }}m$
Substituting the values in the equation we get,
${v^2} - 0 = 2 \times 9.8 \times 2 = 39.2$
Square root of we get,
$v = \sqrt {39.2} = 6.26$
The velocity of the particle at the height of $3.0{\text{ }}m$from the ground is ${\text{6}}{\text{.26 }}\dfrac{m}{s}$.

Note: It must be noted that the acceleration of the particle is considered as acceleration due to gravity as the particle is acting on the Y-axis where there is the acceleration due to gravity which acts on the particle. The initial velocity of the particle is $0{\text{ }}\dfrac{m}{s}$ as it is at rest position initially. The distance covered by the particle should be considered from the starting point.