Question
Question: A body of mass \[2{\rm{ kg}}\] has an initial speed \[5{\rm{ m}}{{\rm{s}}^{ - 1}}\]. A force acts on...
A body of mass 2kg has an initial speed 5ms−1. A force acts on it for 4 seconds in the direction of motion. The force time graph is shown in figure. The final speed of the body is
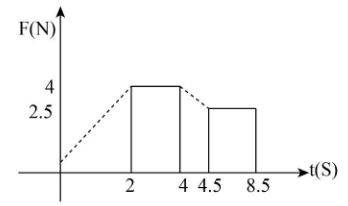
- 8.5ms−1
- 11ms−1
- 14.31ms−1
- 4.31ms−1
Solution
The area of force-time curve of the given body gives us the value of change in momentum of the body. We know that the momentum of the body is equal to the product of its mass and velocity. We will use these concepts to deduce the final velocity of the given body.
Complete step by step answer:
Given:
The mass of the body is m=2kg.
The initial speed of the body is Vi=5ms−1.
The time for action of the force is t=4s.
We know that the area of the force-time graph gives us the value of change in momentum of the body. By closely observing the graph we will find that there are two triangles and the rest are rectangles. We know that the area of a triangle is the half of the product of its base and height and the product of two adjacent sides gives the area of a rectangle. Therefore, we can write the area of the given graph to know the difference between the initial and final of the given body as below:
We know that the momentum of a body is given by the product of its mass and velocity; therefore, its unit is kilogram-metre per second so that we can write:
ΔP=23.625kgms−1
We can also write the above expression as the difference between final and initial momentum.
{P_i} = \left( {2{\rm{ kg}}} \right)\left( {5{\rm{ m}}{{\rm{s}}^{ - 1}}} \right)\\
\Rightarrow{P_i} = 10{\rm{ kgm}}{{\rm{s}}^{ - 1}}
{P_f} = 23.625{\rm{ kgm}}{{\rm{s}}^{ - 1}} + 10{\rm{ kgm}}{{\rm{s}}^{ - 1}}\\
\Rightarrow{P_f} = 33.625{\rm{ kgm}}{{\rm{s}}^{ - 1}}
33.625{\rm{ kgm}}{{\rm{s}}^{ - 1}} = \left( {2{\rm{ kg}}} \right){V_f}\\
\therefore{V_f} = 16.812{\rm{ m}}{{\rm{s}}^{ - 1}}
