Question

A body of mass 2 kg is moving towards the north with a speed of 4m/s. A force of 4 N is applied on it towards the west. Displacement of the body 2 seconds after the force is applied
(A) $4\sqrt{5}m$
(B) $4\sqrt{2}m$
(C) $5\sqrt{4}m$
(D) $5\sqrt{2}m$

Answer 1

Here we are given with the body of given mass moving with a given velocity (magnitude and direction both are given) and force is applied to it. We can solve this using vectors.

Complete step by step answer:
Mass, m= 2 kg
Velocity, v= 4 m/s towards north
Force, F= 4 N towards the west
Representing this

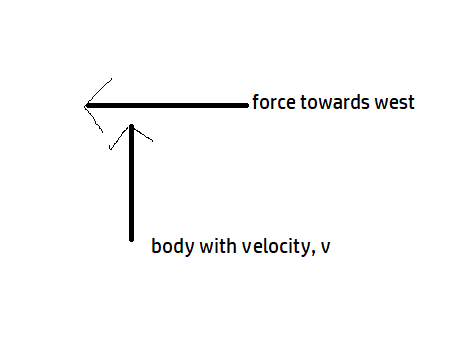
The velocity vector and the force vector both are perpendicular to each other, so the angle between them is $90{{}^{0}}$
Force acts on the body for 2 s
Displacement due north will be s= $4\times 2=8m$
Say this as ${{s}_{1}}=8m$----------(1)

Using second law, $\overrightarrow{F}=m\overrightarrow{a}$
$4=2\overrightarrow{a}$
$\overrightarrow{a}=2m{{s}^{-2}}$ and this is towards the west. Now to find displacement due to the west we have to use the equation of motion.
$s=ut+\dfrac{a{{t}^{2}}}{2}$
Here u is the velocity towards the west but the body was moving towards north, so, u=0
$s=\dfrac{2\times {{2}^{2}}}{2}=4m$
So the displacement due west is 4 m in two seconds
Say this as ${{s}_{2}}=8m$-------(2)
From eq (1) and (2) both are vectors and both are perpendicular to each other. We have to use the parallelogram law of vector addition to add two vectors.

& {{s}_{net}}=\sqrt{s_{1}^{2}+s_{2}^{2}} \\\ & =\sqrt{{{4}^{2}}+{{8}^{2}}} \\\ & =\sqrt{16+64} \\\ & =\sqrt{80} \\\ & =4\sqrt{5}m \\\ \end{aligned}$$ Hence, the net displacement of the body is $$4\sqrt{5}m$$ So, the correct option is (A) **Note:** Because displacement is a vector quantity we can add it algebraically. For vectors, we have to consider their directions. Here the vectors were perpendicular so the cosine component vanishes.